题目内容
正四棱锥P-ABCD的底面边长为2，侧棱长为
，且它的五个顶点都在同一球面上，则此球的表面积为_____________.
答案：9π 【解析】本题考查组合体知识．如图在直角三角形PAE中有：
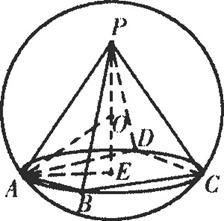
PE2+AE2=PA2即(R+OE)2+(
)2=(
)2
R+OE=2 ①，又在直角三角形OAE中OE2+AE2=R2
OE2+(
)2=R2，将①式代入解得：R=
，故其表面积S=4πR2=9π．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
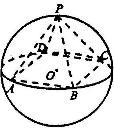如图，正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上，点P在球面上，如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
（2009•温州一模）如图是正四棱锥P-ABCD的三视图，其中正视图是边长为1的正三角形，则这个四棱锥的表面积是（ ）