题目内容
正四棱柱ABCD-A1B1C1D1内接于一个球,且底面ABCD边长为1,高AA1为
,则A、B两点的球面距离为( )
| 2 |
| A、π | ||
B、
| ||
C、
| ||
D、
|
分析:已知正四棱柱ABCD-A1B1C1D1的底面ABCD边长为1,高AA1=
,它的八个顶点都在同一球面上,那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.则易得球的半径. 根据球面距离的定义,应先算出球面两点对球心的张角,再乘以球的半径即可.
| 2 |
解答:解:已知正四棱柱ABCD-A1B1C1D1的底面ABCD边长为1,高AA1=
,它的八个顶点都在同一球面上,
那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.
正四棱柱对角线AC1=2,
则球的半径为1.
根据球面距离的定义,可得∠AOB=
;
则A,B两点的球面距离为
•1=
.
那么球的半径是 1;A,B两点的球面距离为
.
故选C.
| 2 |
那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.
正四棱柱对角线AC1=2,
则球的半径为1.
根据球面距离的定义,可得∠AOB=
| π |
| 3 |
则A,B两点的球面距离为
| π |
| 3 |
| π |
| 3 |
那么球的半径是 1;A,B两点的球面距离为
| π |
| 3 |
故选C.
点评:(1)涉及到多面体与球相关的“切”“接”问题时,关键是抓住球心的位置.球心是球的灵魂.
(2)根据球面距离的定义,应先算出球面两点对球心的张角,再乘以球的半径.这是通性通法.
(2)根据球面距离的定义,应先算出球面两点对球心的张角,再乘以球的半径.这是通性通法.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
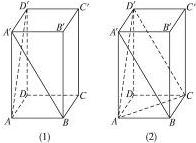 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是