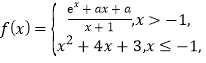题目内容
【题目】设函数![]() .
.
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)求导得![]() ,故根据
,故根据![]() 的符号可判断函数的单调性.(2)结合(1)中的函数的单调性求解,当
的符号可判断函数的单调性.(2)结合(1)中的函数的单调性求解,当![]() 时
时![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,且
单调递减,且![]() ,故要有两个零点,则需
,故要有两个零点,则需![]() ,解不等式可得结果;当
,解不等式可得结果;当![]() 时,可得
时,可得![]() 单调递增,而
单调递增,而![]() ,所以
,所以![]() 在
在![]() 上有一个零点0,不合题意.由此可得所求范围为
上有一个零点0,不合题意.由此可得所求范围为![]() .
.
详解:( 1)∵![]() ,
,
∴![]() .
.
令![]() ,则
,则![]() .
.
∴![]() 有两不等实根
有两不等实根![]() ,
,![]() .
.
且当![]() 或
或![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)解法1:
①当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
∵![]() 在
在![]() 上有两个零点,且
上有两个零点,且![]() ,
,
∴![]() ,解得
,解得![]() .
.
②当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,而
单调递增,而![]() ,所以因为
,所以因为![]() 在
在![]() 上有一个零点0.
上有一个零点0.
综上得当![]() 在
在![]() 上有两个零点时,实数
上有两个零点时,实数![]() 的取值范围为
的取值范围为![]() .
.
解法2:
①当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
又![]() ,
,
∴![]() 在
在![]() 上有一个零点0.
上有一个零点0.
②当![]() 时,由(1)得
时,由(1)得![]() ,
,![]() .
.
(ⅰ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 单调递增.
单调递增.
又![]() ,
,
∴![]() 在
在![]() 上只有一个零点.
上只有一个零点.
(ⅱ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∵![]() ,
,
∴若![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() ,解得
,解得![]() .
.
综上得当![]() 在
在![]() 上有两个零点时,实数
上有两个零点时,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: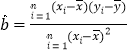 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)