题目内容
【题目】设命题p：实数x满足|x﹣1|＞a其中a＞0；命题q：实数x满足 
＜1
（1）若命题p中a=1，且p∧q为真，求实数x的取值范围；
（2）若￢p是q的必要不充分条件，求实数a的取值范围．
【答案】
（1）解：当a=1时，p：x＞2或x＜0，q：﹣2＜x＜3；
又p∧q真，∴p，q都为真；
∴由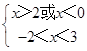 
得﹣2＜x＜0或2＜x＜3；
∴实数x取值范围为（﹣2，0）∪（2，3）
（2）解：p：|x﹣1|＞a，∴x＜1﹣a或x＞1+a，a＞0，￢p：1﹣a≤x≤1+a，a＞0；
∵￢p是q的必要不充分条件；
∴ 
；
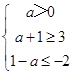∴a≥3；
∴实数a的取值范围为[3，+∞）
【解析】（1）a=1时，得出命题p：x＞2，或x＜0，命题q：﹣2＜x＜3，而由p∧q为真得到p，q都为真，从而解不等式组 
即得实数x的取值范围；（2）先求出命题￢p：x＜1﹣a，或x＞1+a，a＞0，从而由￢p是q的必要不充分条件得到 
，解该不等式组即得实数a的取值范围．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
