题目内容
已知抛物线 的焦点为
的焦点为 ,
, 为
为 上异于原点的任意一点,过点
上异于原点的任意一点,过点 的直线
的直线 交
交 于另一点
于另一点 ,交
,交 轴的正半轴于点
轴的正半轴于点 ,且有
,且有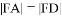 .当点
.当点 的横坐标为3时,
的横坐标为3时,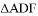 为正三角形.
为正三角形.
(1)求 的方程;
的方程;
(2)延长 交抛物线于点
交抛物线于点 ,过点
,过点 作抛物线的切线
作抛物线的切线 ,求证:
,求证: .
.
练习册系列答案
相关题目
题目内容
已知抛物线 的焦点为
的焦点为 ,
, 为
为 上异于原点的任意一点,过点
上异于原点的任意一点,过点 的直线
的直线 交
交 于另一点
于另一点 ,交
,交 轴的正半轴于点
轴的正半轴于点 ,且有
,且有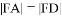 .当点
.当点 的横坐标为3时,
的横坐标为3时,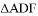 为正三角形.
为正三角形.
(1)求 的方程;
的方程;
(2)延长 交抛物线于点
交抛物线于点 ,过点
,过点 作抛物线的切线
作抛物线的切线 ,求证:
,求证: .
.