题目内容
已知函数f(x)= 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。
(Ⅰ)求实数a,b的值;
(Ⅱ)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(Ⅲ)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根个数。
(Ⅰ) ;(Ⅱ)实数c的取值范围是(0,+∞) ;(Ⅲ)当k>
;(Ⅱ)实数c的取值范围是(0,+∞) ;(Ⅲ)当k>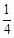 或k<0时,方程f(x)=kx有一个实根;当k=
或k<0时,方程f(x)=kx有一个实根;当k=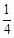 或k=0时,方程f(x)=kx有两个实根;当0<k<
或k=0时,方程f(x)=kx有两个实根;当0<k<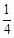 时,方程f(x)=kx有三个实根。
时,方程f(x)=kx有三个实根。
解析试题分析:(Ⅰ)由于两个极值点都小于零,故对 在
在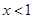 求导,,即当
求导,,即当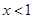 时,
时,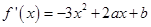 ,依题意,由
,依题意,由 可求实数
可求实数 的值;(Ⅱ)由(Ⅰ)可求得
的值;(Ⅱ)由(Ⅰ)可求得 ,依题意A,B的横坐标互为相反数,不妨设
,依题意A,B的横坐标互为相反数,不妨设 ,分
,分 与
与 讨论,利用
讨论,利用 是直角,
是直角, ,即可求得实数
,即可求得实数 的取值范围;(Ⅲ)由方程
的取值范围;(Ⅲ)由方程 ,知
,知 ,可知
,可知 一定是方程的根,
一定是方程的根, ,方程等价于
,方程等价于 ,构造函数
,构造函数 ,分
,分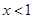 且
且 与
与 两类讨论,即可确定
两类讨论,即可确定 的实根的个数.
的实根的个数.
试题解析:(Ⅰ)当x<1时,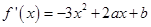 .
.
因为函数f(x)在x=0,x= 处存在极值,所以
处存在极值,所以
解得a=1,b=0. (3分)
(Ⅱ)由(1)得
根据条件知A,B的横坐标互为相反数,不妨设A(-t,t3+t2), B(t,f(t)(t>0). (4分)
若t<1,则f(t)=-t3+t2,
由∠AOB是直角得 ·
· =0,即-t2+(t3+t2)(-t3+t2)=0,
=0,即-t2+(t3+t2)(-t3+t2)=0,
即t4-t2+1=0.此时无解; (5分)
若t≥1,则f(t)=c(et―1―1).由于AB的中点在y轴上,且∠AOB是直角,
所以B点不可能在x轴上,即t≠1.
同理 ·
· =0, 即-t2+( t3+t2)·c(et―1―1)=0,
=0, 即-t2+( t3+t2)·c(et―1―1)=0,
整理后得  . (7分)
. (7分)
因为函数y=(t+1)(et-1―1)在t>1上的值域是(0, +∞),
所以实数c的取值范围是(0, +∞). (8分)
(3)由方程f(x)=kx,
知
因为0一定是方程的根, (9分)
所以仅就x≠0时进行研究:
方程等价于
构造函数 (10分)
(10分)
对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,当x= 时取得最大值
时取得最大值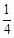 ,其值域是(-∞, 0)∪(0,
,其值域是(-∞, 0)∪(0, 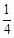 ]; (11分)
]; (11分)
对于x≥1部分,函数 ,由
,由 ,
,
知函数g(x)在(1, +∞)上单调递增,则g(x) [0,+
[0,+ ) (13分)
) (13分)
所以, ①当k>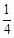 或k<0时,方程f(x)=kx有一个实根;
或k<0时,方程f(x)=kx有一个实根;
②当k=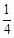 或k=0时,方程f(x)=kx有两个实根;
或k=0时,方程f(x)=kx有两个实根;
③当0<k<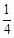 时,方程f(x)=kx有三个实根。 (14分)
时,方程f(x)=kx有三个实根。 (14分)
考点:利用导数研究函数的极值;根的存在性及根的个数判断.

 , 在
, 在 处取得极小值2.
处取得极小值2. 的解析式;
的解析式; , 若对于任意
, 若对于任意 ,总存在
,总存在 , 使得
, 使得 , 求实数
, 求实数  的取值范围.
的取值范围. .
. ,求
,求 在点
在点 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 ,
, .
. 与
与 在
在 处相切,试求
处相切,试求 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;

 .
. .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数). ,试判断函数
,试判断函数 在区间
在区间 上的单调性;
上的单调性; ,当
,当 时,试比较
时,试比较 ,
, (
( ),求k的取值范围,并证明
),求k的取值范围,并证明 .
. ,如果函数
,如果函数 恰有两个不同的极值点
恰有两个不同的极值点 ,
, ,且
,且 .
. ;(Ⅱ)求
;(Ⅱ)求 的最小值,并指出此时
的最小值,并指出此时 的值.
的值. (其中
(其中 为常数).
为常数).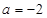 时,求函数
时,求函数 的最值;
的最值;