题目内容
(13分)已知函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)讨论函数 的单调性.
的单调性.
(1)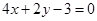 .
.
(2)当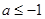 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;当
单调递增;当 时,
时,  在
在 和
和 单调递增,在
单调递增,在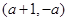 单调递减;当
单调递减;当 时,
时, 在
在 单调递增;当
单调递增;当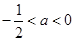 时,
时, 在
在 和
和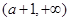 单调递增,在
单调递增,在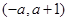 单调递减;当
单调递减;当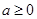 时,
时, 在
在 单调递减,在
单调递减,在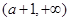 单调递增。
单调递增。
解析试题分析:(1)通过求导数,确定得到切线的斜率,利用直线方程的点斜式,即得解.
(2)求导数,求驻点,得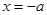 或
或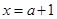 .分以下情况讨论.
.分以下情况讨论.
1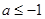 ;2
;2 ;3
;3 ;4
;4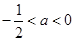 ; 5
; 5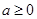 等,明确函数
等,明确函数 的单调区间.
的单调区间.
试题解析:(1) 时,
时,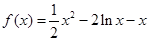 ,
, ,
, ,
,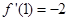 ,所以所求切线方程为
,所以所求切线方程为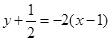 ,即
,即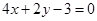 .
.
(2)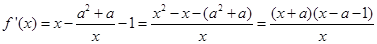 ,令
,令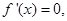 得
得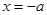 或
或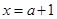 .
.
1当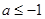 时,
时, ,所以
,所以 在
在 单调递减,在
单调递减,在 单调递增;
单调递增;
2当 时,
时,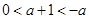 ,所以
,所以 在
在 和
和 单调递增,在
单调递增,在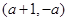 单调递减;
单调递减;
3当 时,
时, ,所以
,所以 在
在 单调递增;
单调递增;
4当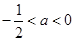 时,
时, ,所以
,所以 在
在 和
和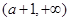 单调递增,在
单调递增,在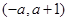 单调递减;
单调递减;
5当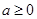 时,
时, ,所以
,所以 在
在 单调递减,在
单调递减,在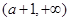 单调递增。
单调递增。
综上,当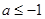 时,
时, 在
在 单调递减,在
单调递减,在 单调递增;当
单调递增;当 时,
时,  在
在 和
和 单调递增,在
单调递增,在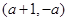 单调递减;当
单调递减;当 时,
时, 在
在 单调递增;当
单调递增;当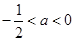 时,
时, 在
在 和
和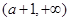 单调递增,在
单调递增,在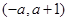 单调递减;当
单调递减;当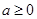 时,
时, 在
在 单调递减,在
单调递减,在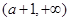 单调递增。
单调递增。
考点:导数的几何意义,应用导数研究函数的单调性.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 ;
; 在
在 上单调递增;
上单调递增; ,若直线PQ∥x轴,求P,Q两点间的最短距离.
,若直线PQ∥x轴,求P,Q两点间的最短距离. .
. 在
在 和
和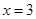 处的切线互相平行,求
处的切线互相平行,求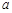 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意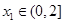 ,均存在
,均存在 ,使得
,使得 ,求
,求 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数). ,试判断函数
,试判断函数 在区间
在区间 上的单调性;
上的单调性; ,当
,当 时,试比较
时,试比较 ,
, (
( ),求k的取值范围,并证明
),求k的取值范围,并证明 .
. =
= 。
。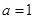 时,求函数
时,求函数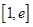 上的最小值;
上的最小值;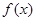 =
=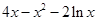 ,
,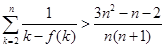 (
(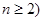 ),参考数据:
),参考数据: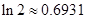 。(13分)
。(13分) ,如果函数
,如果函数 恰有两个不同的极值点
恰有两个不同的极值点 ,
, ,且
,且 .
. ;(Ⅱ)求
;(Ⅱ)求 的最小值,并指出此时
的最小值,并指出此时 的值.
的值. 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 ),
), (单位:弧度).
(单位:弧度).
 的函数;
的函数; ,
, .
. ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围; .
.