Question

18．如右图，棱长为1的正方体ABCD-A₁B₁C₁D₁中，P为线段A₁B上的动点（不含端点），下列结论：
①D₁B与平面ABCD所成角为45°
②DC₁⊥D₁P
③二面角 A-A₁P-D₁的大小为90°
④AP+PD₁的最小值为$\sqrt{2+\sqrt{2}}$
其中正确结论的序号是②③④．（写出所有正确结论的序号）

Answer 1

分析 ①由题意知，DD₁⊥平面ABCD，D₁B在平面ABCD上的投影为DB，所以D₁B与平面ABCD所成角即∠D₁BD，错误；
②先证明DC₁⊥A₁B，A₁D₁⊥DC₁即DC₁⊥平面A₁BD₁，所以DC₁⊥D₁P，正确；
③易知平面A₁PD₁⊥平面AA₁P，所以二面角 A-A₁P-D₁的大小为90°，正确；
④将面BAA₁与面A₁D₁CB展开，线段A₁D₁即为最小值，正确．

解答 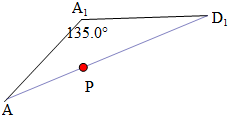解：①，由题意知，DD₁⊥平面ABCD，D₁B在平面ABCD上的投影为DB，所以D₁B与平面ABCD所成角即∠D₁BD，
易知DD₁=1，D₁B=$\sqrt{3}$，DB=$\sqrt{2}$，且∠D₁DB=90°，所以显然D₁B与平面ABCD所成角不是45°，错误；
②，∵DC₁⊥D₁C且D₁C∥A₁B∴DC₁⊥A₁B
∵A₁D₁⊥平面DCC₁D₁，DC₁∈平面DCC₁D₁∴A₁D₁⊥DC₁∴DC₁⊥平面A₁BD₁
∵D₁P∈平面A₁BD₁∴DC₁⊥D₁P，正确；
③，易知A₁D₁⊥平面ABB₁A₁，即A₁D₁⊥平面AA₁P，
∵A₁D₁∈平面A₁PD₁∴平面A₁PD₁⊥平面AA₁P∴二面角 A-A₁P-D₁的大小为90°，正确；
④，将面BAA₁与面A₁D₁CB展开，如图所示，线段A₁D₁即为最小值，利用余弦定理解得A₁D₁=$\sqrt{2+\sqrt{2}}$，正确．
故答案为：②③④

点评 本题考查了线面所成角的算法，余弦定理，二面角的求法，线线垂直的证明，属于中档题．