题目内容
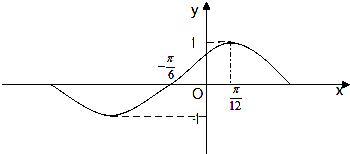
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的部分图象如图所示,将y=f(x)的图象向右平移
个单位后得到函数y=g(x)的图象.
(1)求函数y=g(x)的解析式;
(2)若△ABC的三边为a、b、c成单调递增等差数列,且g(B)=
(B<
),求cosA-cosC的值.
| π |
| 2 |
| π |
| 4 |
(1)求函数y=g(x)的解析式;
(2)若△ABC的三边为a、b、c成单调递增等差数列,且g(B)=
| ||
| 2 |
| π |
| 3 |

分析:(1)利用周期求ω,利用最高点的坐标,求出φ的值,再利用图象平移,可求函数y=g(x)的解析式;
(2)先求出B,再令cosA-cosC=t,则(sinA+sinC)2+(cosA-cosC)2=2+t2,从而可得结论.
(2)先求出B,再令cosA-cosC=t,则(sinA+sinC)2+(cosA-cosC)2=2+t2,从而可得结论.
解答:解:(1)由图知:
=π,ω=2,
∵f(
)=sin(2•
+φ)=1,
∴
+φ=
+2kπ,即φ=
+2kπ,
由于|φ|<
,∴φ=
,
∴f(x)=sin(2x+
),
∴函数y=g(x)的解析式为g(x)=sin[2(x-
)+
]=sin(2x-
).
(2)由于a,b,c成等差,且B<
,
∴g(B)=sin(2B-
)=
,
∵2B-
∈(-
,
),2B-
=
,∴∠B=
,
∴2sinB=sinA+sinC=
,
令cosA-cosC=t,
则(sinA+sinC)2+(cosA-cosC)2=2+t2,
∴t2=-2cos(A+C)=
,
由于t>0,∴t=2
.
| 2π |
| ω |
∵f(
| π |
| 12 |
| π |
| 12 |
∴
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
由于|φ|<
| π |
| 2 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
∴函数y=g(x)的解析式为g(x)=sin[2(x-
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
(2)由于a,b,c成等差,且B<
| π |
| 3 |
∴g(B)=sin(2B-
| π |
| 6 |
| ||
| 2 |
∵2B-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
∴2sinB=sinA+sinC=
| 2 |
令cosA-cosC=t,
则(sinA+sinC)2+(cosA-cosC)2=2+t2,
∴t2=-2cos(A+C)=
| 2 |
由于t>0,∴t=2
| 1 |
| 4 |
点评:本题考查函数解析式的确定,考查图象的平移,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 函数
函数