题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 的图象在
的图象在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 上没有零点,求实数
上没有零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,存在实数
时,存在实数![]() 使得
使得![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】分析:(1)先根据导数几何意义得切线斜率,再根据两点间斜率公式列等式,解得![]() 的值;(2)先求导数,根据a讨论导数零点情况,再根据对应单调性确定函数值域,最后根据无零点确定最小值大于零或最大值小于零,解得结果,(3)先根据
的值;(2)先求导数,根据a讨论导数零点情况,再根据对应单调性确定函数值域,最后根据无零点确定最小值大于零或最大值小于零,解得结果,(3)先根据![]() ,解得
,解得![]() ,代入
,代入![]() 得
得![]() ,再转化为一元函数:
,再转化为一元函数:![]() 最后利用导数证明h(t)< 0成立.
最后利用导数证明h(t)< 0成立.
详解:(1)因为f ′(x)=![]() -a,所以k=f ′(1)=1-a,
-a,所以k=f ′(1)=1-a,
又因为f(1)=-a-b,所以切线方程为y+a+b=(1-a)(x-1),
因为过点(2,0),所以a+b=1-a,即2a+b=1.
(2)当b=0时,f(x)=lnx-ax,所以f ′(x)=![]() -a=
-a=![]() .
.
10若a≤0,则f ′(x)>0,所以f(x)在(![]() ,+∞)上递增,所以f(x)>f(
,+∞)上递增,所以f(x)>f(![]() )=-1-
)=-1-![]() ,
,
因为函数y=f(x)在(![]() ,+∞)上没有零点,所以-1-
,+∞)上没有零点,所以-1-![]() ≥0,即a≤-e;
≥0,即a≤-e;
20若a>0,由f ′(x)=0,得x=![]() .
.
①当![]() ≤
≤![]() 时,即a≥e时,f ′(x)<0,f(x)在(
时,即a≥e时,f ′(x)<0,f(x)在(![]() ,+∞)上递减,
,+∞)上递减,
所以f(x)<f(![]() )=-1-
)=-1-![]() <0,符合题意,所以a≥e;
<0,符合题意,所以a≥e;
②当![]() >
>![]() 时,即0<a<e时,若
时,即0<a<e时,若![]() <x<
<x<![]() ,f ′(x)<0,f(x)在(
,f ′(x)<0,f(x)在(![]() ,
,![]() )上递增;
)上递增;
若x>![]() ,f ′(x)>0,f(x)在(
,f ′(x)>0,f(x)在(![]() ,+∞)上递减,
,+∞)上递减,
所以f(x)在x=![]() 处取得极大值,即为最大值,
处取得极大值,即为最大值,
要使函数y=f(x)在(![]() ,+∞)上没有零点,
,+∞)上没有零点,
必须满足f(![]() )=ln
)=ln![]() -1=-lna-1<0,得a>
-1=-lna-1<0,得a>![]() ,所以
,所以![]() <a<e.
<a<e.
综上所述,实数a的取值范围是a≤-e或a>![]() .
.
(3)不妨设0<x1<x2,
由f(x1)=f(x2),得lnx1-ax1-b=lnx2-ax2-b,
因为a>0,所以![]() .
.
又因为![]() ,f ′(x)在(0,+∞)上递减,且f ′(
,f ′(x)在(0,+∞)上递减,且f ′(![]() )=0,
)=0,
故要证![]() ,只要证
,只要证![]() ,
,
只要证![]() ,只要证
,只要证![]() ,
,
只要证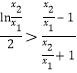 (*),
(*),
令![]() ,记
,记![]() ,
,
则![]() ,
,
所以h(t)在(1,+∞)上递减,所以h(t)< h(1)=0,
所以(*)成立,所以原命题成立.

