题目内容
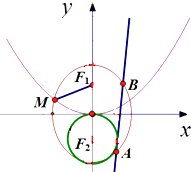
【题目】已知曲线C的极坐标方程为ρ=6sinθ,以极点O为原点,极轴为x轴的非负半轴建立直角坐标系,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)直线l与曲线C交于B,D两点,当|BD|取到最小值时,求a的值.
【答案】
(1)解:曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,化为直角坐标方程:x2+y2=6y,配方为:x2+(y﹣3)2=9,圆心C(0,3),半径r=3.
直线l的参数方程为 ![]() (t为参数),消去参数t可得:x﹣ay+a+1=0
(t为参数),消去参数t可得:x﹣ay+a+1=0
(2)解:由直线l经过定点P(﹣1,1),此点在圆的内部,
因此当CP⊥l时,|BD|取到最小值,则kCPkl= ![]() ×kl=﹣1,解得kl=﹣
×kl=﹣1,解得kl=﹣ ![]() .
.
∴ ![]() =﹣
=﹣ ![]() ,解得a=﹣2
,解得a=﹣2
【解析】(1)曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程.直线l的参数方程为 ![]() (t为参数),消去参数t可得普通方程.(2)由直线l经过定点P(﹣1,1),此点在圆的内部,因此当CP⊥l时,|BD|取到最小值,利用kCPkl=﹣1,解得kl , 即可得出.
(t为参数),消去参数t可得普通方程.(2)由直线l经过定点P(﹣1,1),此点在圆的内部,因此当CP⊥l时,|BD|取到最小值,利用kCPkl=﹣1,解得kl , 即可得出.

【题目】学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的![]() ,对教师管理水平给出好评的学生人数为总数的
,对教师管理水平给出好评的学生人数为总数的![]() ,其中对教师教学水平和教师管理水平都给出好评的有120人.
,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的![]() 列联表:
列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
请问是否可以在犯错误概率不超过0.001的前提下,认为教师教学水平好评与教师管理水平好评有关?
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量![]() .
.
①求对教师教学水平和教师管理水平全好评的人数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
| 认为作业量大 | 认为作业量不大 | 合计 |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
(Ⅲ)若视频率为概率,在全校随机抽取4人,其中“认为作业量大”的人数记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附:![]()