题目内容
【题目】设椭圆![]() ,定义椭圆
,定义椭圆![]() 的“相关圆
的“相关圆![]() ”的方程为
”的方程为![]() ,若抛物线
,若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,且椭圆
的一个焦点重合,且椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形.
短轴的一个端点和其两个焦点构成直角三角形.
(1)求椭圆![]() 的方程和“相关圆
的方程和“相关圆![]() ”的方程;
”的方程;
(2)若直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
①求证:![]() ;
;
②求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() (2)①证明见解析; ②
(2)①证明见解析; ②![]()
【解析】
(1)由抛物线焦点为![]() 及椭圆
及椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形,即可求得
短轴的一个端点和其两个焦点构成直角三角形,即可求得![]() ,从而可得到本题答案;
,从而可得到本题答案;
(2)①分直线l的斜率存在和不存在两种情况考虑,求出![]() 的值,即可得到本题结论;②算出直线斜率不存在时
的值,即可得到本题结论;②算出直线斜率不存在时![]() 的值,以及斜率存在时
的值,以及斜率存在时![]() 的最大值,通过比较大小,即可得到本题答案.
的最大值,通过比较大小,即可得到本题答案.
(1)易知抛物线焦点为![]() ,
,
又由![]() 的一个短轴端点与两焦点构成直角三角形,
的一个短轴端点与两焦点构成直角三角形,
可得![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,
,
相关圆![]() 的方程为
的方程为![]() .
.
(2)①(i)![]() 斜率不存在时,可得
斜率不存在时,可得![]() 的方程为
的方程为![]() ,
,
联立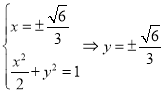 ,
,
即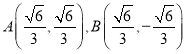 或
或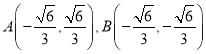
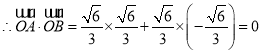 ,
,
![]() ;
;
(ii)斜率存在时,可设![]() 的方程为
的方程为![]() ,
,![]() ,联立
,联立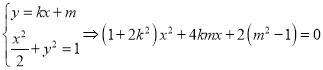 ,
,
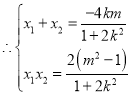 ,
,
由圆![]() 与
与![]() 相切可得
相切可得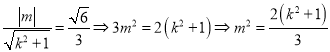 ,
,
![]()
![]()
![]()
![]() ,
,
![]() 由(i)(ii)知,
由(i)(ii)知,![]() 恒成立.
恒成立.
②![]() 斜率不存在时,由①可得
斜率不存在时,由①可得![]() ,
,
![]() 斜率存在时,由①可得
斜率存在时,由①可得
![]()
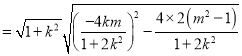
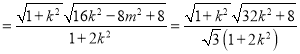 ,
,
令![]() ,则
,则![]() ,
,
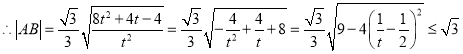 ,
,
(当且仅当![]() 时取“
时取“![]() ”)
”)
![]() .
.

练习册系列答案
相关题目



