题目内容
某校从高二年级学生中随机抽取60名学生,将其会考的政治成绩(均为整数)分成六段: 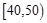 ,
,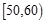 ,…,
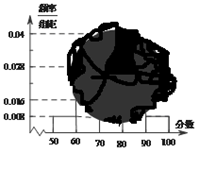
,…,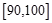 后得到如下频率分布直方图.
后得到如下频率分布直方图.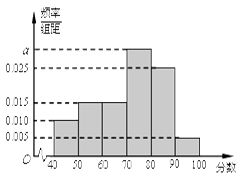
(Ⅰ)求图中 的值
的值
(Ⅱ)根据频率分布直方图,估计该校高二年级学生政治成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上(含 80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
(1)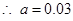
(2)71(3)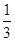
解析试题分析:解:(Ⅰ)分数在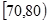 内的频率为:
内的频率为: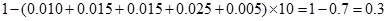
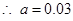 3分
3分
(Ⅱ)平均分为: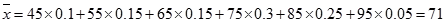 7分
7分
(Ⅲ)由题意,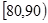 分数段的人数为:
分数段的人数为: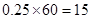 人
人 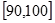 分数段的人数为:
分数段的人数为: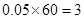 人; 9分
人; 9分
∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,
∴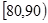 分数段抽取5人,
分数段抽取5人,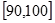 分数段抽取1人,设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件
分数段抽取1人,设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件 ,概率为
,概率为
考点:直方图和古典概型
点评:主要是分析题意,理解题意,结合直方图和古典概型概率来求解,属于基础题。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于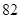 为正品,小于
为正品,小于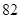 为次品.现随机抽取这两种元件各
为次品.现随机抽取这两种元件各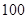 件进行检测,检测结果统计如下:
件进行检测,检测结果统计如下:
| 测试指标 | 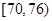 | 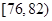 | 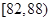 | 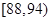 | 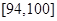 |
| 元件A | 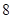 | 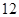 | 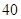 | 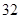 | 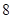 |
| 元件B | 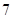 | 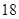 | 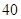 | 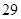 | 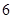 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记
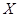 为生产1件元件A和1件元件B所得的总利润,求随机变量
为生产1件元件A和1件元件B所得的总利润,求随机变量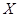 的分布列和数学期望;
的分布列和数学期望;(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
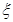 ,求
,求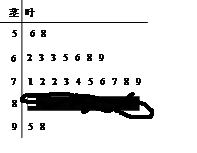
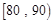 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中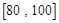 之间的学生中任选两人进行某项研究,求至少有一人分数在
之间的学生中任选两人进行某项研究,求至少有一人分数在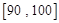 之间的概率.
之间的概率. ,求随机变量
,求随机变量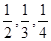 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。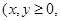 且
且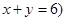 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.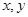 的值;
的值;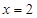 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数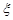 的期望
的期望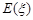 .
.