题目内容
正四棱锥V-ABCD的五个顶点在同一个球面上,若其底面边长为4,侧棱长为2
,则AB两点的球面距为( )
| 6 |
分析:设球的半径为R,利用正四棱锥的性质和球的性质,结合勾股定理列方程,求得球半径,根据余弦定理和球面距离的公式,即可求得结论.
解答:解:设外接球球心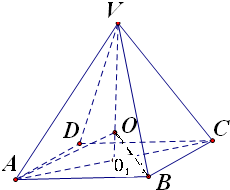 为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
∵正方形ABCD边长为4,∴对角线AC=4
,O1A=
AC=2
∵VO1⊥平面ABCD,
∴Rt△VO1A中,VO1=4
设外接球半径为R,则Rt△OO1A中,OA=R,O1O=4-R
∴R2=(4-R)2+(2
)2,解之得:R=3
∴△AOB中,cos∠AOB=
∴∠AOB=arccos
所以AB两点的球面距为R×∠AOB=3arccos
故选B.
 为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB
为O,正方形ABCD中心为O1,连接VO1,则球心O在VO1上,连接AC、OA、OB∵正方形ABCD边长为4,∴对角线AC=4
| 2 |
| 1 |
| 2 |
| 2 |
∵VO1⊥平面ABCD,
∴Rt△VO1A中,VO1=4
设外接球半径为R,则Rt△OO1A中,OA=R,O1O=4-R
∴R2=(4-R)2+(2
| 2 |
∴△AOB中,cos∠AOB=
| 1 |
| 9 |
∴∠AOB=arccos
| 1 |
| 9 |
所以AB两点的球面距为R×∠AOB=3arccos
| 1 |
| 9 |
故选B.
点评:本题考查球内接正四棱锥,考查球面距离,确定球的半径是关键,属于中档题.

练习册系列答案
相关题目
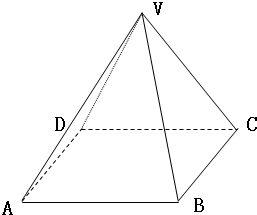 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.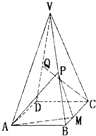 (2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2
(2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2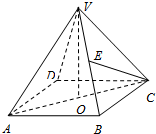 (2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.
(2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.