题目内容
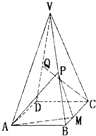（2013•乌鲁木齐一模）在正四棱锥V-ABCD中，P，Q分别为棱VB，VD的中点，点 M 在边 BC 上，且 BM：BC=1：3，AB=2| 3 |
（I ）求证CQ丄AP；
（II）求二面角B-AP-M的余弦值．
分析：（I）设正方形ABCD的中心为O，N为AB的中点，R为BC的中点，分别以ON、OR、OV所在直线为x轴、y轴、z轴建立空间直角坐标系，分别算出V、A、B、C、D、M、P、Q各点的坐标，从而得到向量
和
的坐标，通过计算得到
•
=0，从而得到
⊥
，即可证出CQ丄AP；
（II）由（I）所建立的坐标系，算出
=（0，2
，0），
=（-
，2
，0），利用垂直向量数量积为0的方法算出平面BAP的法向量为
=（
，0，1），同理得到平面APM的法向量为
=（3，1，0），最后运用空间向量的夹角公式加以计算，得到
、
的夹角余弦，即为二面角B-AP-M的余弦值．
| AP |
| CQ |
| AP |
| CQ |
| AP |
| CQ |
（II）由（I）所建立的坐标系，算出
| AB |
| 3 |
| AM |
2
| ||
| 3 |
| 3 |
| n1 |
| 10 |
| n2 |
| n1 |
| n2 |
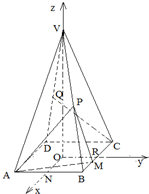
解答：解：设正方形ABCD的中心为O，N为AB的中点，R为BC的中点，分别以ON、OR、OV所在直线为x轴、y轴、z轴，
如图建立空间直角坐标系，
在Rt△VOB中，可得OV=
，
则V（0，0，
），A（
，-
，0），B（
，
，0），C（-
，
，0）
D（-
，-
，0），M（
，
，0），P（
，
，
），
Q（-
，-
，
）．
于是
=（-
，
，
），
=（0，2
，0），
=（-
，2
，0），
=（
，-
，
）．
（Ⅰ）∵
•
=-
×
+
×（-
）+
×
=0，
∴
⊥
，即CQ丄AP； …（6分）
（Ⅱ）设平面BAP的法向量为
=（a，b，c），
由
，得
，取a=
，得
=（
，0，1），
同理可得平面APM的法向量为
=（3，1，0），
设二面角B-AP-M的平面角为θ，则cosθ=
=
． …（12分）
如图建立空间直角坐标系，
在Rt△VOB中，可得OV=| 30 |
则V（0，0，
| 30 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
D（-
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
Q（-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
于是
| AP |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| AB |
| 3 |
| AM |
2
| ||
| 3 |
| 3 |
| CQ |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
（Ⅰ）∵
| AP |
| CQ |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AP |
| CQ |
（Ⅱ）设平面BAP的法向量为
| n1 |
由
|
|
| 10 |
| n1 |
| 10 |
同理可得平面APM的法向量为
| n2 |
设二面角B-AP-M的平面角为θ，则cosθ=
| ||||
|
|
3
| ||
| 11 |
点评：本题给出正四棱锥，求证两条直线异面垂直并求二面角的余弦之值，着重考查了用空间向量证明线线垂直和求平面与平面的所成角等知识，属于中档题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
（2013•乌鲁木齐一模）函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象如图所示，其 中A，B两点之间的距离为5，则f（x）的递增区间是（ ）