题目内容
（2011•广州模拟）在正四棱锥V-ABCD中，底面正方形ABCD的边长为1，侧棱长为2，则异面直线VA与BD所成角的大小为（ ）
分析：连接AC，交BD于O，连接VO，先在正方形ABCD中证出对角线AC、BD互相垂直，再在三角形VBD中，根据VB=VD和O为BD中点，证出VO、BD互相垂直，最后根据直线与平面垂直的判定理证出BD⊥平面ACV，从而BD⊥VA，即异面直线VA与BD所成角大小为
．
| π |
| 2 |
解答：解：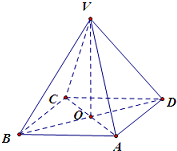
连接AC，交BD于O，连接VO
∵四边形ABCD是正方形，
∴AC⊥BD，O为BD的中点
又∵正四棱锥V-ABCD中，VB=VD
∴VO⊥BD
∵AC∩VO=O，AC、VO?平面ACV
∴BD⊥平面ACV
∵VA?平面ACV
∴BD⊥VA
即异面直线VA与BD所成角等于
，
故选D
连接AC，交BD于O，连接VO∵四边形ABCD是正方形，
∴AC⊥BD，O为BD的中点
又∵正四棱锥V-ABCD中，VB=VD
∴VO⊥BD
∵AC∩VO=O，AC、VO?平面ACV
∴BD⊥平面ACV
∵VA?平面ACV
∴BD⊥VA
即异面直线VA与BD所成角等于
| π |
| 2 |
故选D
点评：本题以求正四棱锥中异面直线所成角为载体，着重考查了直线与平面垂直的判定与性质，以及异面垂直的概念，属于基础题．
练习册系列答案
相关题目