题目内容
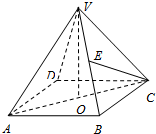 (2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.
(2009•虹口区一模)如图,正四棱锥V-ABCD的高和底面的边长均相等,E是棱VB的中点.(1)求证:AC⊥VD;
(2)(文科)求:异面直线CE和VD的夹角大小;
(理科)求:二面角E-AC-B的大小.
分析:(1)连接AB,CD交于O,通过证明AC⊥BD,AC⊥VO证得AC⊥面VDB,再证明AC⊥VD
(2)(文科)可知OE∥VD,所以∠CEO (或其补角)即为异面直线CE和VD的夹角.在△CEO 中求解即可.
(理科)由(1)得出AC⊥OE,AC⊥OB,所以∠EOB为二面角E-AC-B的平面角,在△EOH 求解即可
(2)(文科)可知OE∥VD,所以∠CEO (或其补角)即为异面直线CE和VD的夹角.在△CEO 中求解即可.
(理科)由(1)得出AC⊥OE,AC⊥OB,所以∠EOB为二面角E-AC-B的平面角,在△EOH 求解即可
解答:解:(1)证明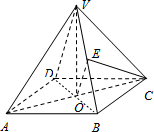 连接AB,CD交于O
连接AB,CD交于O
则AC⊥BD,AC⊥VO,且BD∩VO=O,∴AC⊥面VDB,又VD?VDB∴AC⊥VD.
(2)(文科)
∵E是棱VB的中点,所以OE∥VD,∴∠CEO (或其补角)即为异面直线CE和VD的夹角.设高和底面的边长均为2,则在△VBC中,VC2=VO2+OC2=22+
2=6,VC=
.
cos∠CVB=
=
=
,CE2=VC2+VE2-2VC×VE×cos∠CVB=6+
-2×
×
×
=
在△CEO 中,cos∠CEO=
=
=
∴∠CEO=arccos
.即异面直线CE和VD的夹角大小为arccos
.
(理科)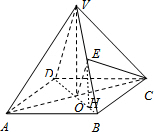
由(1)AC⊥面VDB,,∴AC⊥OE,AC⊥OB,∴∠EOB为二面角E-AC-B的平面角,取BO中点 H,则EH∥VO,EH⊥面ABCD 且 EH=1,
在直角△EOH,tan∠EOB=
=
=
,,∴∠EOB=arctan
,即二面角E-AC-B的大小为arctan
.
 连接AB,CD交于O
连接AB,CD交于O则AC⊥BD,AC⊥VO,且BD∩VO=O,∴AC⊥面VDB,又VD?VDB∴AC⊥VD.
(2)(文科)
∵E是棱VB的中点,所以OE∥VD,∴∠CEO (或其补角)即为异面直线CE和VD的夹角.设高和底面的边长均为2,则在△VBC中,VC2=VO2+OC2=22+
| 2 |
| 6 |
cos∠CVB=
| VC2+VB2-CB2 |
| 2×VB×VC |
| 6+6-4 | ||||
2×
|
| 2 |
| 3 |
| 6 |
| 4 |
| 6 |
| ||
| 2 |
| 2 |
| 3 |
| 7 |
| 2 |
在△CEO 中,cos∠CEO=
| EO2+ EC2-OC2 |
| 2×EO×EC |
| ||||||||
2×
|
| ||
| 7 |
| ||
| 7 |
| ||
| 7 |
(理科)

由(1)AC⊥面VDB,,∴AC⊥OE,AC⊥OB,∴∠EOB为二面角E-AC-B的平面角,取BO中点 H,则EH∥VO,EH⊥面ABCD 且 EH=1,
在直角△EOH,tan∠EOB=
| EH |
| OH |
| 1 | ||||
|
| 2 |
| 2 |
| 2 |
点评:本小题主要考查空间线面关系、异面直线的夹角、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
相关题目