题目内容
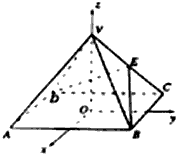
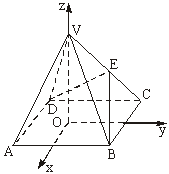
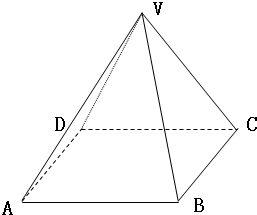 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.(Ⅰ)求COS<
| BE |
| DE |
(Ⅱ)当k取何值时,∠BED是二面角B-VC-D的平面角,并求二面角B-VC-D的余弦值.
分析:(Ⅰ)给出各点的坐标,求出两个向量
=(-
, -
,
),
=(
,
,
),利用数量积公式即可求解;
(Ⅱ)假设,∠BED是二面角B-VC-D的平面角可得
⊥
,
•
=0,
•
=0,代入坐标解得引入的参数的关系,再代入二面角B-VC-D的余弦公式即可求值
| BE |
| 3a |
| 2 |
| a |
| 2 |
| H |
| 2 |
| DE |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
(Ⅱ)假设,∠BED是二面角B-VC-D的平面角可得
| BE |
| CV |
| BE |
| CV |
| DE |
| CV |
解答:解:(I)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),
E(-
,
,
)由此得:
=(-
, -
,
),
=(
,
,
)
∴
•
=-
+
(3分)
|
=|
|=
(5分)
由向量的数量积公式有:
cos<
,
>=
=
=
(7分)
(II)若∠BED是二面角B-VC-D的平面角,则
⊥
∴
•
=0,
•
=0(8分)
由C(-a,a,0),V(0,0,h)有
=(a,-a,h)
又
=(-
, -
,
),
∴
•
=a2+
=0解得:h=
a(10分)
∴cos<
,
>=
=
=
=-
(12分)
VA=
=2a又VA=kAB且AB=2a
从而k=1反之成立(13分)
因此当k=1时,∠BED是二面角B-VC-D的平面角,且二面角B-VC-D的余弦值为-
.(14分)
E(-
| a |
| 2 |
| a |
| 2 |
| h |
| 2 |
| BE |
| 3a |
| 2 |
| a |
| 2 |
| H |
| 2 |
| DE |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
∴
| BE |
| DE |
| 3a 2 |
| 2 |
| h 2 |
| 4 |
|
| BE| |
| DE |
| 1 |
| 2 |
| 10a2+h2 |
由向量的数量积公式有:
cos<
| BE |
| DE |
| ||||
|
|
-
| ||||||||
|
| -6a2+h2 |
| 10a2+h2 |
(II)若∠BED是二面角B-VC-D的平面角,则
| BE |
| CV |
∴
| BE |
| CV |
| DE |
| CV |
由C(-a,a,0),V(0,0,h)有
| CV |
又
| BE |
| 3a |
| 2 |
| a |
| 2 |
| H |
| 2 |
∴
| BE |
| CV |
| h2 |
| 2 |
| 2 |
∴cos<
| BE |
| DE |
| ||||
|
|
| -6a2+h2 |
| 10a2+h2 |
-6a2+(
| ||
10a2+ (
|
| 1 |
| 3 |
VA=
| VO2+OA2 |
从而k=1反之成立(13分)
因此当k=1时,∠BED是二面角B-VC-D的平面角,且二面角B-VC-D的余弦值为-
| 1 |
| 3 |
点评:本题察利用空间向量求二面角以及利用空间向量寻求某角是二面角平面角的条件,考查数形结合、化归转化的数学思想和方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
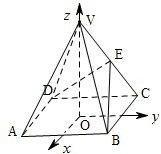 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.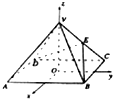 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.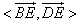 ;
;