题目内容
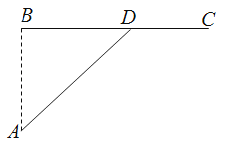
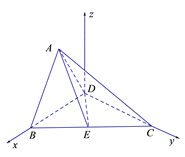
【题目】如图,在直角梯形![]() 中,
中, ![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
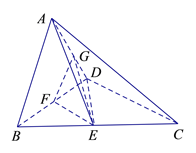
,连接![]() 得到如图
得到如图![]() 所示的几何体.
所示的几何体.

(1)求证; ![]() 平面
平面![]() ;
;
(2)若![]() 二面角
二面角![]() 的平面角的正切值为
的平面角的正切值为![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:(I)由平面与名垂直的性质定理可得![]() ⊥平面
⊥平面![]() . 由折叠前后均有
. 由折叠前后均有![]() ⊥
⊥![]() ,
, ![]() ∩
∩![]() ,可得
,可得![]() ⊥平面
⊥平面![]() ;(Ⅱ) 由(Ⅰ)可得二面角
;(Ⅱ) 由(Ⅰ)可得二面角![]() 的平面角为∠
的平面角为∠![]() ,又依题意
,又依题意![]() ,可得
,可得![]() ,依次求得
,依次求得![]() .,以下由两种解法:1.建立空间直角坐标系,求得相应点的坐标,求得平面
.,以下由两种解法:1.建立空间直角坐标系,求得相应点的坐标,求得平面![]() 的法向量
的法向量![]() 和平面
和平面![]() 的法向量
的法向量![]() ,则问题可求:2.利用相关的立体几何知识,证明二面角
,则问题可求:2.利用相关的立体几何知识,证明二面角![]() 的平面角为
的平面角为![]() ,然后利用面几何知识求得二面角
,然后利用面几何知识求得二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:
(Ⅰ) 因为平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() ⊥
⊥![]() ,所以
,所以![]() ⊥平面
⊥平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ⊥
⊥![]() .
.
又因为折叠前后均有![]() ⊥
⊥![]() ,
, ![]() ∩
∩![]() ,
,
所以![]() ⊥平面
⊥平面![]() .
.
(Ⅱ) 由(Ⅰ)知![]() ⊥平面
⊥平面![]() ,所以二面角
,所以二面角![]() 的平面角为∠
的平面角为∠![]() .
.
又![]() ⊥平面
⊥平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ⊥
⊥![]() .
.
依题意![]() .
.
因为![]() ,所以
,所以![]() .
.
设![]() ,则
,则![]() .
.
依题意△![]() ~△
~△![]() ,所以
,所以![]() ,即
,即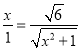 .
.
解得![]() ,故
,故![]() .
.
法1:如图所示,建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
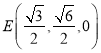 ,
, 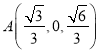 ,
,
所以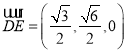 ,
, 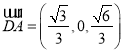 .
.
由(Ⅰ)知平面![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量
的法向量![]()
由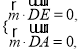 得
得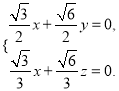
令![]() ,得
,得![]() ,
,
所以![]() .
.
所以![]() .
.
由图可知二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
法2 :因为![]() ⊥平面
⊥平面![]() ,
,
过点![]() 作
作![]() //
// ![]() 交
交![]() 于
于![]() ,
,
则![]() ⊥平面
⊥平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() ⊥
⊥![]() .
.
过点![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,连接
,连接![]() ,
,
所以![]() ⊥平面
⊥平面![]() ,因此
,因此![]() ⊥
⊥![]() .
.
所以二面角![]() 的平面角为
的平面角为![]() .
.
由平面几何知识求得
![]() ,
, ![]() ,
,
所以![]() .
.
所以cos∠![]() =
=![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.