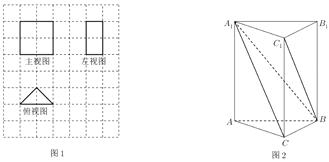
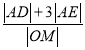题目内容
【题目】已知x=1是函数f(x)=mx3﹣3(m+1)x2+nx+1的一个极值点,其中m,n∈R,m<0.
(1)求m与n的关系表达式;
(2)求f(x)的单调区间;
(3)当x∈[﹣1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
【答案】(1)n=3m+6.(2)f(x)在(﹣∞,1![]() )单调递减,在(1
)单调递减,在(1![]() ,1)单调递增,在(1,+∞)单调递减.(3)
,1)单调递增,在(1,+∞)单调递减.(3)![]() m<0.
m<0.
【解析】
(1)求出f′(x),因为x=1是函数的极值点,所以得到f'(1)=0求出m与n的关系式;
(2)令f′(x)=0求出函数的极值点,讨论函数的增减性确定函数的单调区间;
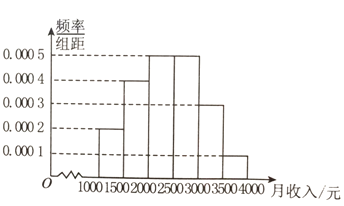
(3)由题意知f′(x)>3m,分x=1和x≠1,当x≠1时g(t)=t![]() ,求出g(t)的最小值.要使
,求出g(t)的最小值.要使![]() (x﹣1)
(x﹣1)![]() 恒成立即要g(t)的最小值
恒成立即要g(t)的最小值![]() ,解出不等式的解集求出m的范围.
,解出不等式的解集求出m的范围.
(1)f′(x)=3mx2﹣6(m+1)x+n.
因为x=1是f(x)的一个极值点,所以f'(1)=0,即3m﹣6(m+1)+n=0.
所以n=3m+6.
(2)由(1)知f′(x)=3mx2﹣6(m+1)x+3m+6=3m(x﹣1)[x﹣(1![]() )]
)]
当m<0时,有1>1![]() ,当x变化时f(x)与f'(x)的变化如下表:
,当x变化时f(x)与f'(x)的变化如下表:
x | (﹣∞,1 | 1 | (1 | 1 | (1,+∞) |
f′(x) | <0 | 0 | >0 | 0 | <0 |
f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
由上表知,当m<0时,f(x)在(﹣∞,1![]() )单调递减,在(1
)单调递减,在(1![]() ,1)单调递增,在(1,+∞)单调递减.
,1)单调递增,在(1,+∞)单调递减.
(3)由已知,得f′(x)>3m,即3m(x﹣1)[x﹣(1![]() )]>3m,
)]>3m,
∵m<0.∴(x﹣1)[x﹣1(1![]() )]<1.(*)
)]<1.(*)
①x=1时.(*)式化为0<1恒成立.
∴m<0.
②x≠1时∵x∈[﹣1,1],∴﹣2≤x﹣1<0.
(*)式化为![]() (x﹣1)
(x﹣1)![]() .
.
令t=x﹣1,则t∈[﹣2,0),记g(t)=t![]() ,
,
则g(t)在区间[﹣2,0)是单调增函数.∴g(t)min=g(﹣2)=﹣2![]() .
.
由(*)式恒成立,必有![]()
![]() m,又m<0.∴
m,又m<0.∴![]() m<0.
m<0.
综上①②知![]() m<0.
m<0.

【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
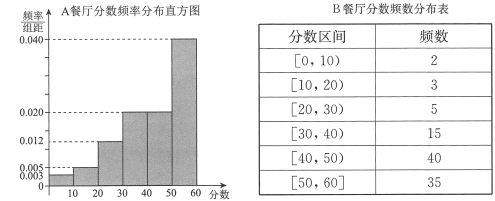
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对![]() 餐厅评价“满意度指数”为0的人数;
餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在, ![]() 两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对
两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对![]() 餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”比对![]() 餐厅评价的“满意度指数”高的概率;
餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.