题目内容
12.已知$\overline{z}$是z的共轭复数,若$\overline{z}$=1+i(i是虚数单位),则$\frac{2}{z}$=( )| A. | 1-i | B. | -1-i | C. | -1+i | D. | 1+i |
分析 由$\overline{z}$=1+i求得z,代入$\frac{2}{z}$后由代数形式的乘除运算化简得答案.
解答 解:∵$\overline{z}$=1+i,∴z=1-i,
则$\frac{2}{z}$=$\frac{2}{1-i}=\frac{2(1+i)}{(1-i)(1+i)}=\frac{2(1+i)}{2}=1+i$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,是基础题.

练习册系列答案
相关题目
3.已知a∈($\frac{3π}{2}$,2π),且sin(a+β)sinβ+cos(a+β)cosβ=$\frac{1}{3}$,则sina的值( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
20.图是一算法的程序框图,若输出结果为S=5040,则在判断框中应填入的条件是( )
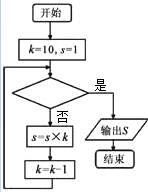

| A. | k≤9 | B. | k≤8 | C. | k≤7 | D. | k≤6 |
17.为了得到函数y=cosx,x∈R的图象,只需把y=cos$\frac{x}{5}$,x∈R上所有的点的( )
| A. | 横坐标伸长为原来的5倍,纵坐标不变 | |
| B. | 横坐标缩短为原来的$\frac{1}{5}$倍,纵坐标不变 | |
| C. | 纵坐标伸长为原来的5倍,横坐标不变 | |
| D. | 纵坐标缩短为原来的$\frac{1}{5}$倍,横坐标不变 |
4.若复数z满足:z+|z|=1+2i,则z的虚部为( )
| A. | 2i | B. | 1 | C. | 2 | D. | i |
1.若$a={3^{0.4}},b={log_π}3,c={log_3}sin\frac{3}{π}$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |