题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
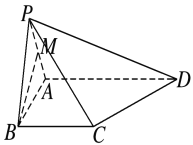
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)16.
【解析】
(1)取![]() 中点
中点![]() ,证明
,证明![]() 为平行四边形,得到
为平行四边形,得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ;(2)对三棱锥
;(2)对三棱锥![]() 进行等体积转化,转化为求
进行等体积转化,转化为求![]() 的体积.过
的体积.过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,证明
,证明![]() 为三棱锥
为三棱锥![]() 的高并求出求出其长度,求出
的高并求出求出其长度,求出![]() 的面积,得到三棱锥
的面积,得到三棱锥![]() 的体积,即三棱锥
的体积,即三棱锥![]() 的体积.
的体积.
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,作
,作![]() ,
,
则![]() ,易知ABCH为平行四边形,有
,易知ABCH为平行四边形,有![]() .
.
![]() 为
为![]() 的中位线,
的中位线,
![]() ,且
,且![]() .
.
又![]() ,且
,且![]() ,
,
![]() ,且
,且![]() ,则
,则![]() 为平行四边形,
为平行四边形,
![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)解:过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]()
又![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() 为三棱锥
为三棱锥![]() 的高,
的高,
![]() ,
,![]() 为
为![]() 中点,
中点,![]()
![]() ,
,![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]()
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
![]()
![]()
![]() 为平行四边形
为平行四边形
![]()
![]() ,
,
![]() ,
,
![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某高校共有10000人,其中男生7500人,女生2500人,为调查该校学生每则平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).调查部分结果如下![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 35 | ||
每周平均体育运动时间超过4小时 | 30 | ||
总计 | 200 |
(1)完成上述每周平均体育运动时间与性别的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 把握认为“该校学生的每周平均体育运动时间与性别有关”;
把握认为“该校学生的每周平均体育运动时间与性别有关”;
(2)已知在被调查的男生中,有5名数学系的学生,其中有2名学生每周平均体育运动时间超过4小时,现从这5名学生中随机抽取2人,求恰有1人“每周平均体育运动时间超过4小时”的概率.
附: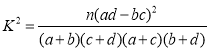 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |