题目内容
16.已知函数f(x)=2x3-6x-m,x∈R.(1)求函数f(x)的单调区间;
(2)若函数f(x)在R上只有一个零点,求常数m的取值范围.
分析 (1)先求出函数的导数,解关于导函数的不等式,从而求出其单调区间.
(2)由题意得f(1)>0,或f(-1)<0,从而求出m的范围.
解答 解:(1)∵函数f(x)=2x3-6x-m,
∴f′(x)=6x2-6=6(x2-1),
令f′(x)>0,解得:x>1或x<-1,
令f′(x)<0,解得:-1<x<1,
∴函数f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)由(1)得:函数f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减,
∴f(x)极大值=f(-1),f(x)极小值=f(1),
若函数f(x)在R上只有一个零点,
画出函数的草图,如图示: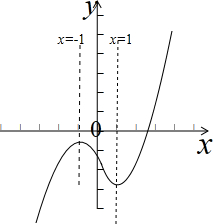 ,或
,或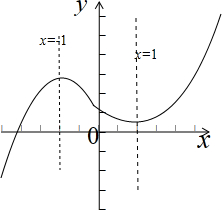 ,
,
只需f(-1)=-2+6-m<0,或f(1)=2-6-m>0解得:m>4或m<-4.
点评 本题考查了函数的单调性,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
6. 如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
(1)A∈l,(2)C∈α.则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为( )
 如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:(1)A∈l,(2)C∈α.则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 1+$\sqrt{5}$ | D. | $\sqrt{10}$ |
4.已知集合A={x|x2-2x>0},B={x|log2(x+1)<1},则A∩B等于( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (-1,0) |
11.已知某产品连续4个月的广告费xi(千元)与销售额yi(万元)(i=1,2,3,4)满足$\underset{\stackrel{4}{∑}}{i=1}{x}_{i}=18$,$\underset{\stackrel{4}{∑}}{i=1}{y}_{i}=14$,若广告费用x和销售额y之间具有线性相关关系,且回归直线方程为$\stackrel{∧}{y}$=0.8x+a,那么广告费用为6千元时,可预测的销售额为( )
| A. | 3.5万元 | B. | 4.7万元 | C. | 4.9万元 | D. | 6.5万元 |
8.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
| A. | m⊥α,n⊥β,且α⊥β,则m⊥n | B. | m∥α,n∥β,且α∥β,则m∥n | ||
| C. | m⊥α,n?β,m⊥n,则α⊥β | D. | m?α,n?α,m∥β,n∥β,则α∥β |
5.已知点O为双曲线C的对称中心,过点O的两条直线l1与l2的夹角为60°,直线l1与双曲线C相交于点A1,B1,直线l2与双曲线C相交于点A2,B2,若使|A1B1|=|A2B2|成立的直线l1与l2有且只有一对,则双曲线C离心率的取值范围是( )
| A. | ($\frac{2\sqrt{3}}{3}$,2] | B. | [$\frac{2\sqrt{3}}{3}$,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |