题目内容
已知二次函数f(x)有两个零点0和-2,且f(x)最小值是-1,函数g(x)与f(x)的图像关于原点对称.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在区间[-1,1]上是增函数,求实数λ的取值范围.
(1)f(x)=x2+2x. g(x)=-x2+2x
(2)(-∞,0]
(2)(-∞,0]
试题分析:(1)依题意,设f(x)=ax(x+2)=ax2+2ax(a>0).
f(x)图像的对称轴是x=-1,∴f(-1)=-1,
即a-2a=-1,∴a=1,∴f(x)=x2+2x.
∵函数g(x)的图像与f(x)的图像关于原点对称,
∴g(x)=-f(-x)=-x2+2x.
(2)由(1)得h(x)=x2+2x-λ(-x2+2x)=(λ+1)x2+2(1-λ)x.
①当λ=-1时,h(x)=4x满足在区间[-1,1]上是增函数;
②当λ<-1时,h(x)图像对称轴是x=
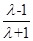 ,
,则
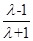 ≥1,又λ<-1,解得λ<-1;
≥1,又λ<-1,解得λ<-1;③当λ>-1时,同理需
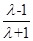 ≤-1,
≤-1,又λ>-1,解得-1<λ≤0.
综上,满足条件的实数λ的取值范围是(-∞,0].
点评:主要是考查了待定系数法求解函数解析式,以及二次函数性质的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -1)
-1) 
 在
在 上的单调;
上的单调; 上的值域是
上的值域是 的值.
的值. g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.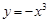
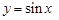
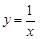
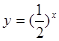
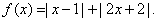
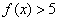 ;
;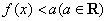 的解集为空集,求
的解集为空集,求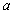 的取值范围.
的取值范围. 的值域为[0,+
的值域为[0,+ ),则
),则 的最小
的最小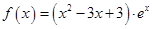 ,设
,设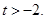
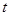 的取值范围,使得函数
的取值范围,使得函数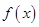 在
在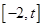 上为单调函数;
上为单调函数;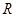 上的函数
上的函数 是最小正周期为
是最小正周期为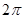 的偶函数,当
的偶函数,当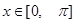 时,
时,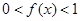 ,且在
,且在 上单调递减,在
上单调递减,在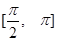 上单调递增,则函数
上单调递增,则函数 在
在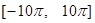 上的零点个数为 .
上的零点个数为 .