题目内容
已知f(x)=32x-(k+1)3x+2,当x∈R时,f(x)恒为正值,则k的取值范围是( )
| A.(-∞,-1) | B.(-∞,2 -1) -1) |
C.(-1,2 -1) -1) | D.(-2 -1,2 -1,2 -1) -1) |
B
由f(x)>0得32x-(k+1)·3x+2>0,解得k+1<3x+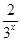 ,而3x+
,而3x+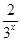 ≥2
≥2
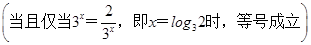 ,
,
∴k+1<2 ,即k<2
,即k<2 -1.
-1.
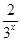 ,而3x+
,而3x+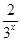 ≥2
≥2
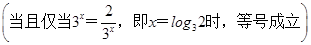 ,
, ∴k+1<2
 ,即k<2
,即k<2 -1.
-1.
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
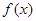 的定义域为
的定义域为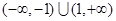 ,对定义域内的任意x,满足
,对定义域内的任意x,满足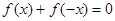 ,当
,当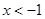 时,
时,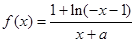 (a为常),且
(a为常),且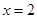 是函数
是函数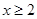 时,不等式
时,不等式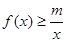 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;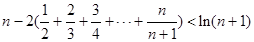




 (k≠0);⑤ y=sinx.
(k≠0);⑤ y=sinx.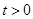 ,函数
,函数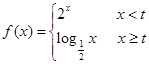 的值域为
的值域为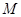 .若
.若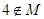 ,则
,则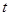 的取值范围是 .
的取值范围是 . 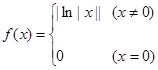 ,则方程
,则方程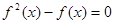 的不相等的实根个数为( )
的不相等的实根个数为( ) 的值
的值