题目内容
14.函数f(x)=lnx-$\frac{1}{2}{x^2}$的极值是-$\frac{1}{2}$.分析 先求出函数的导数,得到函数的单调区间,从而求出函数的极值.
解答 解:f′(x)=$\frac{1}{x}$-x=$\frac{1-{x}^{2}}{x}$,(x>0),
令f′(x)>0,解得:0<x<1,
令f′(x)<0,解得:x>1,
∴函数f(x)在(0,1)递增,在(1,+∞)递减,
∴f(x)极大值=f(1)=$-\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2.如框图,当x1=5,x2=8,p=8.5时,x3=( )
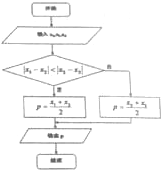

| A. | 6 | B. | 7 | C. | 9 | D. | 10 |
9.过曲线C:y=$\frac{1}{x}$(x>0)上一点P(x0,y0)作曲线C的切线,若切线的斜率为-4,则x0等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
19.数列{an}满足a1=1,an+1=an-3(n∈N*),则a4=( )
| A. | 10 | B. | 8 | C. | -8 | D. | -10 |
6.在等比数列{an}(n∈N*)中,若a1=1,a4=$\frac{1}{8}$,则该数列的前10项和为( )
| A. | 2-$\frac{1}{2^4}$ | B. | 2-$\frac{1}{{2}^{9}}$ | C. | 2-$\frac{1}{{{2^{10}}}}$ | D. | 2-$\frac{1}{{{2^{11}}}}$ |