题目内容
18.已知椭圆E的中心在坐标原点O,其焦点与双曲线C:x2-$\frac{y^2}{2}$=1的焦点重合,且椭圆E的短轴的两个端点与其一个焦点构成正三角形.(Ⅰ)求椭圆E的方程;
(Ⅱ)过双曲线C的右顶点A作直线l与椭圆E交于不同的两点P、Q.设点M(4,3),记直线PM、QM的斜率分别为k1,k2,求证:k1+k2为定值,求出此定值.
分析 (Ⅰ)设方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,确定c,利用椭圆E的短轴的两个端点与其一个焦点构成正三角形,可得a=2b,利用a2=b2+c2,求出a,b,即可求椭圆E的方程;
(Ⅱ)分类讨论,设l的方程为y=k(x-1),代入椭圆方程,利用韦达定理,结合斜率公式,可得结论.
解答 解:(Ⅰ)由题意椭圆的焦点在x轴上,设方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,其左右焦点为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),∴c=$\sqrt{3}$,
∵椭圆E的短轴的两个端点与其一个焦点构成正三角形,
∴a=2b,
∵a2=b2+c2,
∴a=2,b=1,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)①双曲线C右顶点为A(1,0),
当直线l的斜率存在时,设l的方程为y=k(x-1),
代入椭圆方程得(4k2+1)x2-8k2x+4k2-4=0,
设直线l与椭圆E交点P(x1,y1),Q(x2,y2),
则x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+1}$,x1x2=$\frac{4{k}^{2}-4}{4{k}^{2}+1}$,
∴k1+k2=$\frac{3-{y}_{1}}{4-{x}_{1}}+\frac{3-{y}_{2}}{4-{x}_{2}}$=$\frac{24-3({x}_{1}+{x}_{2})+k[2{x}_{1}{x}_{2}-5({x}_{1}+{x}_{2})+8]}{16-4({x}_{1}+{x}_{2})+{x}_{1}{x}_{2}}$=$\frac{24(3{k}^{2}+1)}{12(3{k}^{2}+1)}$=2
②当直线l的斜率不存在时,直线l的方程为x=1,代入椭圆方程可得x=1,y=±$\frac{\sqrt{3}}{2}$.
不妨设P(1,$\frac{\sqrt{3}}{2}$),Q(1,-$\frac{\sqrt{3}}{2}$),则k1+k2=$\frac{3-\frac{\sqrt{3}}{2}}{4-1}+\frac{3+\frac{\sqrt{3}}{2}}{4-1}$=2为定值.
综上所述,k1+k2为定值,定值为2.
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,属于中档题.

| A. | ${C}_{9}^{3}$ | B. | ${C}_{18}^{3}$ | C. | ${C}_{9}^{4}$ | D. | ${C}_{18}^{6}$ |
| A. | (-1,0)∪(0,1) | B. | .(-∞,-1)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-1,1] |
| A. | 若直线a∥b,b?α,则a∥α | B. | 若平面α⊥β,a⊥α,则a∥β | ||
| C. | 若平面α∥β,a?α,b?β,则a∥b | D. | 若a⊥α,b⊥β,a∥b,则α∥β |
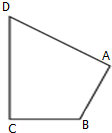 如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )
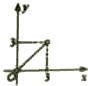
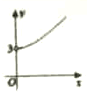
如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )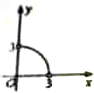

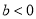 ,且
,且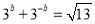 ,则
,则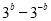 等于( )
等于( )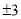 B.-2
B.-2