题目内容
17．已知等差数列{an}的首项为4，公差为2，前n项和为Sn．若Sk-ak+5=44（k∈N*），则k的值为7．分析 由已知写出等差数列的通项公式和求和公式，是基础的计算题．
解答 解：由等差数列{an}的首项为4，公差为2，
得an=4+2（n-1）=2n+2，${S}_{n}=4n+\frac{2n（n-1）}{2}={n}^{2}+3n$，
再由Sk-ak+5=44，得k2+3k-2（k+5）-2=44，解得：k=-8（舍）或k=7．
故答案为：7．
点评 本题考查了等差数列的通项公式，考查了等差数列的前n项和，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
12．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{6}$ | C． | 3 | D． | 2$\sqrt{3}$ |
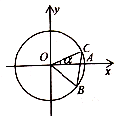如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（$\frac{12}{13}$，-$\frac{5}{13}$），∠AOC=α，若|BC|=1，则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$．
7．已知6枝玫瑰与3枝康乃馨的价格之和大于24元，而4枝玫瑰与4枝康乃馨的价格之和小于20元，那么2枝玫瑰和3枝康乃馨的价格的比较结果是（ ）
| A． | 2枝玫瑰的价格高 | B． | 3枝康乃馨的价格高 | ||
| C． | 价格相同 | D． | 不确定 |