题目内容
7.已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与4枝康乃馨的价格之和小于20元,那么2枝玫瑰和3枝康乃馨的价格的比较结果是( )| A. | 2枝玫瑰的价格高 | B. | 3枝康乃馨的价格高 | ||
| C. | 价格相同 | D. | 不确定 |
分析 设1枝玫瑰和1枝康乃馨的价格分别x,y元,由题意可得:$\left\{\begin{array}{l}{6x+3y>24}\\{4x+4y<20}\end{array}\right.$,化为$\left\{\begin{array}{l}{2x+y>8}\\{-x-y>-5}\end{array}\right.$,设2x-3y=m(2x+y)+n(-x-y)=(2m-n)x+(m-n)y,
令$\left\{\begin{array}{l}{2m-n=2}\\{m-n=-3}\end{array}\right.$,解得m,n,即可得出.
解答 解:设1枝玫瑰和1枝康乃馨的价格分别x,y元,
由题意可得:$\left\{\begin{array}{l}{6x+3y>24}\\{4x+4y<20}\end{array}\right.$,化为$\left\{\begin{array}{l}{2x+y>8}\\{-x-y>-5}\end{array}\right.$,
设2x-3y=m(2x+y)+n(-x-y)=(2m-n)x+(m-n)y,
令$\left\{\begin{array}{l}{2m-n=2}\\{m-n=-3}\end{array}\right.$,解得m=5,n=8,
∴2x-3y=5(2x+y)+8(-x-y)>5×8-5×8=0,
因此2x>3y,
∴2枝玫瑰的价格高.
故选:A.
点评 本题考查了不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
18.设△ABC的内角A,B,C所对的边a,b,c成等比数列,则$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$的取值范围是( )
| A. | (0,+∞) | B. | $({\frac{{\sqrt{5}-1}}{2},+∞})$ | C. | $({0,\frac{{\sqrt{5}+1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ |
12.已知函数$f(x)=\frac{{sinx+cosx+|{sinx-cosx}|}}{2}$,则下列结论正确的是( )
| A. | f(x)是奇函数 | B. | f(x)在$[{0,\frac{π}{2}}]$上递增 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,1] |
19.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的左、右焦点,P为双曲线C右支上一点,且PF2⊥F1F2,PF1与y轴交于点Q,点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,若MQ⊥PF1,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |
16.在复平面内,复数$z=\frac{i}{2+i}$对应的点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
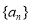 的前
的前 项和为
项和为 ,已知
,已知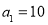 ,
,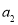 为整数,且
为整数,且 .
. ,求数列
,求数列 的前
的前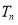 的最大值.
的最大值.