题目内容
6.过点P(-2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形的面积为S,且这样的直线l有且仅有一条,则直线l的方程是x-y+4=0.分析 由过点P(-2,2)且与两坐标轴在第二象限内围成的三角形的面积为S的直线l有且仅有一条,可得P为直线与两坐标轴交点的中点,设出直线方程的截距式,由中点坐标列式求出两截距得答案.
解答 解:设直线l与两坐标轴的交点为A,B,
依题意得P为线段AB的中点,
设l的方程为$\frac{x}{a}+\frac{y}{b}=1$,
则$\left\{\begin{array}{l}{\frac{a}{2}=-2}\\{\frac{b}{2}=2}\end{array}\right.$,即a=-4,b=4,
∴直线l的方程为$\frac{x}{-4}+\frac{y}{4}=1$,即x-y+4=0.
故答案为:x-y+4=0.
点评 本题考查了直线的方程,关键是对题意的理解,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若等比数列{an}满足a1+a3=20,a2+a4=40,则公比q=( )
| A. | 1 | B. | 2 | C. | -2 | D. | 4 |
14.设变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$则z=|x-3y|的取值范围为( )
| A. | [2,8] | B. | [0,8] | C. | [4,8] | D. | [0,4] |
1.若集合M={x|x2>4},N={x|1<x≤3},则N∩(∁RM)=( )
| A. | {x|1<x≤2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|-2≤x≤3} |
11.如图,若N=2015时,则输出的数等于( )
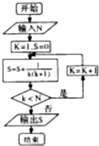

| A. | $\frac{2015}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2016}$ |
18.设△ABC的内角A,B,C所对的边a,b,c成等比数列,则$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$的取值范围是( )
| A. | (0,+∞) | B. | $({\frac{{\sqrt{5}-1}}{2},+∞})$ | C. | $({0,\frac{{\sqrt{5}+1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ |
16.在复平面内,复数$z=\frac{i}{2+i}$对应的点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |