题目内容
2．设$\frac{1+i}{1-i}$=a+bi（i为虚数单位，a，b∈R），则ab的值为0．分析 直接利用复数代数形式的乘除运算化简，由复数相等求得a，b的值，则答案可求．
解答 解：由$\frac{1+i}{1-i}=\frac{（1+i）^{2}}{（1-i）（1+i）}=\frac{2i}{2}=i=a+bi$，
得a=0，b=1．
∴ab=0．
故答案为：0．
点评 本题考查了复数代数形式的乘除运算，考查了复数相等的条件，是基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
13．在二项式（x2-$\frac{1}{x}$）5的展开式中，含x7的项的系数为（ ）
| A． | -10 | B． | 10 | C． | -5 | D． | 5 |
7．定义在R上的函数f（x）对任意x1、x2（x1≠x2）都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s2-2s）≤-f（2t-t2），则当1≤s≤4时，$\frac{t-2s}{s+t}$的取值范围是（ ）
| A． | [-3，-$\frac{1}{2}$） | B． | [-3，-$\frac{1}{2}$] | C． | [-5，-$\frac{1}{2}$） | D． | [-5，-$\frac{1}{2}$] |
14．设变量x，y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$则z=|x-3y|的取值范围为（ ）
| A． | [2，8] | B． | [0，8] | C． | [4，8] | D． | [0，4] |
11．如图，若N=2015时，则输出的数等于（ ）
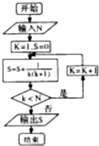
| A． | $\frac{2015}{2014}$ | B． | $\frac{2014}{2015}$ | C． | $\frac{2016}{2015}$ | D． | $\frac{2015}{2016}$ |
12．已知函数$f（x）=\frac{{sinx+cosx+|{sinx-cosx}|}}{2}$，则下列结论正确的是（ ）
| A． | f（x）是奇函数 | B． | f（x）在$[{0，\frac{π}{2}}]$上递增 | C． | f（x）是周期函数 | D． | f（x）的值域为[-1，1] |