题目内容
【题目】在三棱柱ABC﹣A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D. 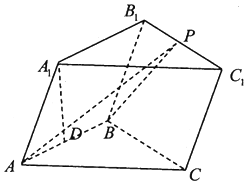
(1)证明:平面AA1B1B⊥平面BB1C1C;
(2)设P为B1C1上一点,且 ![]() ,求二面角A1﹣AB﹣P的正弦值.
,求二面角A1﹣AB﹣P的正弦值.
【答案】
(1)证明:∵点A1在底面ABC的投影为AB的中点D,
∴A1D⊥平面ABC,则A1D⊥BC,
又∵侧面BCC1B1是正方形,∴B1B⊥BC,
∵B1B与A1D在平面ABB1A1上不平行,
∴BC⊥平面ABB1A1,
∴平面AA1B1B⊥平面BB1C1C
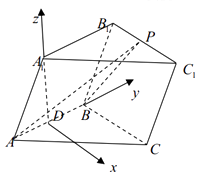
(2)解:如图所示,以点D为坐标原点建立空间直角坐标系,
不妨设菱形边长为2,得D(0,0,0),A(0,﹣1,0),B(0,1,0),
∵D为AB的中点,且有A1D⊥AB,∴AA1=A1B,
又∵平面ABB1A1为菱形,∴△A1AB为等边三角形,
从而 ![]() ,从而
,从而 ![]() ,
,
∴点A1的坐标为 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
又∵ ![]() ,∴
,∴ ![]() ,
,
设平面ABP的法向量为 ![]() ,
,
由 ![]() ,
, ![]() ,
,
得 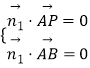 ,即
,即 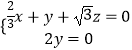 ,
,
令 ![]() ,则
,则 ![]() ,y=0,∴
,y=0,∴ ![]() ,
,
同理求得平面ABB1A1的法向量 ![]() ,
,
∴ 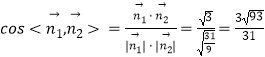 ,
,
∴ ![]() ,
,
从而二面角A1﹣AB﹣P的正弦值为 ![]() .
.
【解析】(1)由点A1在底面ABC的投影为AB的中点D,可得A1D⊥平面ABC,则A1D⊥BC,再由已知可得B1B⊥BC,由线面垂直的判定可得BC⊥平面ABB1A1 , 从而得到平面AA1B1B⊥平面BB1C1C;(2)以点D为坐标原点建立空间直角坐标系,设菱形边长为2,得到对应点的坐标,求出平面ABP与平面ABB1A1的法向量,由两法向量所成角的余弦值求得二面角A1﹣AB﹣P的正弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】某手机厂商推出一款6吋大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(Ⅰ)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
