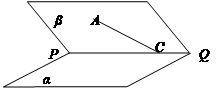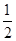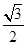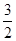题目内容
(如图),具有公共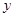 轴的两个直角坐标平面
轴的两个直角坐标平面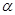 和
和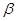 所成的二面角
所成的二面角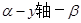 等于
等于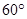 .已知
.已知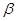 内的曲线
内的曲线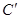 的方程是
的方程是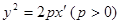 ,求曲线
,求曲线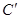 在
在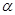 内的射影的曲线方程。
内的射影的曲线方程。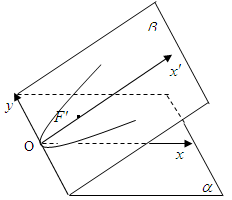
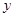 轴的两个直角坐标平面
轴的两个直角坐标平面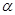 和
和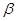 所成的二面角
所成的二面角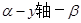 等于
等于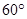 .已知
.已知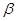 内的曲线
内的曲线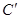 的方程是
的方程是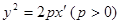 ,求曲线
,求曲线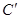 在
在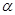 内的射影的曲线方程。
内的射影的曲线方程。
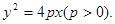
【错解分析】依题意,可知曲线
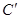 是抛物线,在
是抛物线,在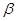 内的焦点坐标是
内的焦点坐标是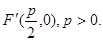
因为二面角
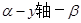 等于
等于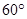 ,且
,且 所以
所以
设焦点
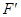 在
在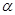 内的射影是
内的射影是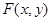 ,那么,
,那么,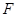 位于
位于 轴上,
轴上,从而
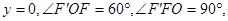
所以
 所以点
所以点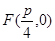 是所求射影的焦点。依题意,射影是一条抛物线,开口向右,顶点在原点。所以曲线
是所求射影的焦点。依题意,射影是一条抛物线,开口向右,顶点在原点。所以曲线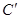 在
在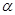 内的射影的曲线方程是
内的射影的曲线方程是
上述解答错误的主要原因是,凭直观误认为F是射影(曲线)的焦点,其次,没有证明默认C/在a内的射影(曲线)是一条抛物线。
【正解】在
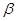 内,设点
内,设点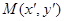 是曲线上任意一点(如图)过点
是曲线上任意一点(如图)过点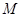 作
作 ,垂足为
,垂足为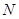 ,过
,过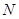 作
作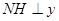 轴,垂足为
轴,垂足为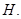 连接
连接 ,则
,则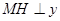 轴。
轴。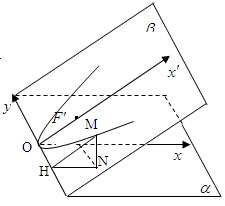
所以
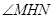 是二面角
是二面角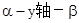 的平面角,依题意,
的平面角,依题意,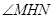
 .
.在

又知
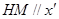 轴(或
轴(或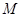 与
与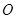 重合),
重合), 轴(或
轴(或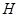 与
与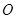 重合),设
重合),设 ,
,则

因为点
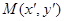 在曲线
在曲线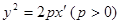 上,所以
上,所以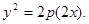
即所求射影的方程为
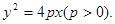

练习册系列答案
相关题目
 中,E为AC中点
中,E为AC中点

 ,
,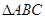 的中心,则直线EF与平面ABC所成的角的正切值是 。
的中心,则直线EF与平面ABC所成的角的正切值是 。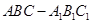 中,侧棱
中,侧棱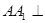 底面
底面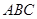 ,
,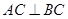 ,
,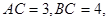
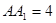 ,
,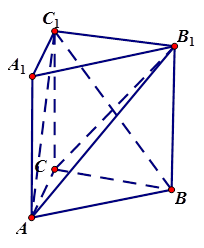
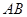 与
与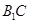 所成角的余弦值;
所成角的余弦值;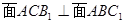
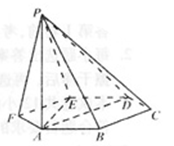
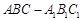 中,
中,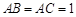 ,
,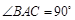 ,且异面直线
,且异面直线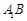 与
与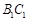 所成的角等于
所成的角等于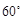 .
.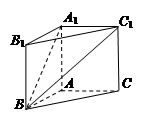
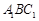 所成的角的大小.
所成的角的大小.