题目内容
三棱柱ABC-A1B1C1中,底面边长和侧棱长都相等,∠BAA1=∠CAA1=60°,则异面直线AB1与BC1所成角的余弦值为________.
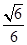
试题分析:设
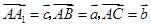 ,棱长为1,则
,棱长为1,则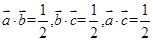 ,
,因为
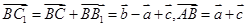 ,
, 所以
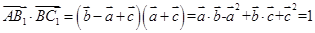 ,
,所以
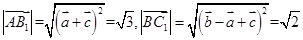 ,
,所以
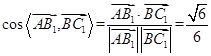 ,所以异面直线
,所以异面直线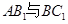 所成角的余弦值为
所成角的余弦值为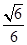 。
。点评:本题主要考查了空间向量在解决立体几何问题中的应用,空间向量基本定理,向量数量积运算的性质及夹角公式的应用,有一定的运算量.

练习册系列答案
相关题目
题目内容
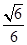
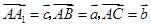 ,棱长为1,则
,棱长为1,则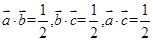 ,
,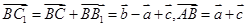 ,
, 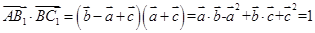 ,
,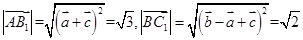 ,
,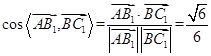 ,所以异面直线
,所以异面直线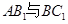 所成角的余弦值为
所成角的余弦值为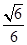 。
。