题目内容
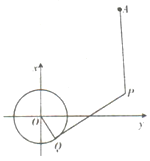
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4sinθ.
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4sinθ.
(Ⅰ)写出直线l和曲线C的普通方程;
(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最小值.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】
(Ⅰ)消去参数可得直线的普通方程y=x-4.极坐标方程化为直角坐标方程可得曲线C的直角坐标方程为x2+(y-2)2=4;
(Ⅱ)由题意利用几何法确定P到直线l的距离的最小值即可.
(Ⅰ)直线l: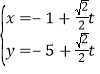 (其中t为参数),消去参数t得普通方程y=x-4.
(其中t为参数),消去参数t得普通方程y=x-4.
由ρ=4sinθ得ρ2=4ρsinθ.
由x=ρcosθ,y=ρsinθ以及x2+y2=ρ2,得
x2+(y-2)2=4;
(Ⅱ)由x2+(y-2)2=4得圆心坐标为(0,2),半径R=2,
则圆心到直线的距离为:d=![]() =3
=3![]() ,
,
而点P在圆上,即O′P+PQ=d(Q为圆心到直线l的垂足),
所以点P到直线l的距离最小值为3![]() -2.
-2.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某地区为了解群众上下班共享单车使用情况,根据年龄按分层抽样的方式调查了该地区50名群众,他们的年龄频数及使用共享单车人数分布如下表:
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
(1)由以上统计数据完成下面的![]() 列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附: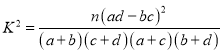 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(2)若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人,再从这6人中随机抽取2人,求这2人中恰好有1人年龄在30~39岁的概率.