题目内容
18.已知x>$\frac{1}{2}$,y>1且xy=e,求t=(2x)lny的最大值.分析 x>$\frac{1}{2}$,y>1且xy=e,可得2x=$\frac{2e}{y}$.对t=(2x)lny两边取对数可得:lnt=lnyln(2x)=lny•$ln\frac{2e}{y}$=-$(lny-\frac{1+ln2}{2})^{2}$+$\frac{(1+ln2)^{2}}{4}$,利用二次函数的单调性即可得出.
解答 解:∵x>$\frac{1}{2}$,y>1且xy=e,
∴2x=$\frac{2e}{y}$.
对t=(2x)lny两边取对数可得:lnt=lnyln(2x)=lny•$ln\frac{2e}{y}$=lny(1+ln2-lny)=-ln2y+(1+ln2)lny=-$(lny-\frac{1+ln2}{2})^{2}$+$\frac{(1+ln2)^{2}}{4}$≤$\frac{(1+ln2)^{2}}{4}$,
∴$t≤{e}^{\frac{(1+ln2)^{2}}{4}}$.当且仅当y=${e}^{\frac{1+ln2}{2}}$,x=${e}^{\frac{1-ln2}{2}}$时取等号.
∴t=(2x)lny的最大值为${e}^{\frac{(1+ln2)^{2}}{4}}$.
点评 本题考查了对数的运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.某组织通过抽样调查(样本容量n=1000),利用2×2列联表和x2统计量研究喜爱古典音乐是否与青年的性别有关.计算得x2=15.02,经查对临界值表知P(x2≥6.635)≈0.01,现判定喜爱古典音乐与性别有关系,那么这种判断出错的可能性为( )
| A. | 0.01 | B. | 0.90 | C. | 0.99 | D. | 0.1 |
9.下列函数中,当0<x1<x2<1时,满足x2f(x1)<x1f(x2)的函数是( )
| A. | f(x)=-x3 | B. | f(x)=lnx | C. | f(x)=x2+1 | D. | f(x)=($\frac{1}{2}$)x |
2.如图所示,输出的结果是( )


| A. | 50 | B. | 20 | C. | 60 | D. | 120 |
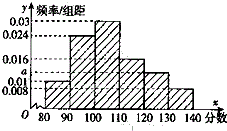 某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (115,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如右图所示的频率分布直方图
某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (115,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如右图所示的频率分布直方图