题目内容
9.下列函数中,当0<x1<x2<1时,满足x2f(x1)<x1f(x2)的函数是( )| A. | f(x)=-x3 | B. | f(x)=lnx | C. | f(x)=x2+1 | D. | f(x)=($\frac{1}{2}$)x |
分析 由条件结合单调性的定义可得函数y=$\frac{f(x)}{x}$在(0,1)为增函数.对选项一一加以分析,运用导数,判断(0,1)内导数符号,即可判断单调性.
解答 解:当0<x1<x2<1时,满足x2f(x1)<x1f(x2)即为
$\frac{f({x}_{1})}{{x}_{1}}$<$\frac{f({x}_{2})}{{x}_{2}}$,
由单调性定义可得,y=$\frac{f(x)}{x}$在(0,1)为增函数.
对于A,$\frac{f(x)}{x}$=-x2在(0,1)递减,不满足条件;
对于B,$\frac{f(x)}{x}$=$\frac{lnx}{x}$的导数为$\frac{1-lnx}{{x}^{2}}$,在(0,1)内导数为正,即有$\frac{f(x)}{x}$在(0,1)递增,满足条件;
对于C,$\frac{f(x)}{x}$=x+$\frac{1}{x}$的导数为1-$\frac{1}{{x}^{2}}$,在(0,1)内导数为负,即有$\frac{f(x)}{x}$在(0,1)递减,不满足条件;
对于D,$\frac{f(x)}{x}$=$\frac{(\frac{1}{2})^{x}}{x}$的导数为$\frac{(\frac{1}{2})^{x}(xln\frac{1}{2}-1)}{x}$,在(0,1)内导数为负,即有$\frac{f(x)}{x}$在(0,1)递减,不满足条件.
故选:B.
点评 本题考查导数的运用:判断单调性,同时考查函数的单调性的运用,注意构造函数和正确求导是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.运行如图所示的程序框图,输出的所有实数对(x,y)所对应的点都在函数( )
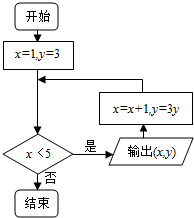

| A. | y=x+2图象上 | B. | y=3x图象上 | C. | y=3x的图象上 | D. | y=3x3图象上 |
4.如图所示是一个程序框图,输出的结果是( )


| A. | 1616 | B. | 1617 | C. | 1716 | D. | 1717 |
14.已知全集U={1,2,3,4,5,6,7},集合∁U(A∪B)={1,3},A∩∁UB={2,4},则集合B等于( )
| A. | {1,3,5,6,7} | B. | {2,4,5,6,7} | C. | {5,6,7} | D. | {1,2,3,4} |
