题目内容
(理科题)(本小题12分)
已知数列{an}是等差数列,a2=3,a5=6,数列{bn}的前n项和是Tn,且Tn+ bn=1.
bn=1.
(1)求数列{an}的通项公式与前n项的和 ;
;
(2)求数列{bn}的通项公式.
(1) 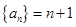 .
. 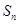 =
=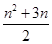 . (2)证明:见解析。
. (2)证明:见解析。
解析试题分析:(1)设{an}的公差为d,进而根据等差数列通项公式表示出a2和a5,求得a1和d,则数列的通项公式和求和公式可得.
(2)根据Tn-Tn-1=bn,整理得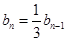 ,判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案..
,判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案..
(1)设{an}的公差为d,则:a2=a1+d,a5=a1+4d. ……………2分
……………2分
∴a1=2,d=1 ……………3分
∴an=2+(n-1)=n+1.…………4分
Sn=na1+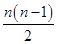 d=
d=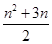 .………………6分
.………………6分
(2)证明:当n=1时,b1=T1,
由T1+ b1=1,得b1=
b1=1,得b1=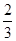 . ………8分
. ………8分
当n≥2时,∵Tn=1- bn,Tn-1=1-
bn,Tn-1=1- bn-1,
bn-1,
∴Tn-Tn-1= (bn-1-bn),……………10分
(bn-1-bn),……………10分
即bn= (bn-1-bn).
(bn-1-bn).
∴bn=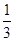 bn-1. …………11分
bn-1. …………11分
∴{bn}是以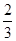 为首项,
为首项,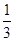 为公比的等比数列.∴bn=
为公比的等比数列.∴bn=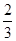 ·(
·(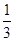 )n-1=
)n-1=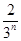 .……………12分
.……………12分
考点:等差数列的通项公式;考查了等差数列的性质和等比数列的判定,等差数列的前n项和;等比数列的通项公式.
点评:先求出等差数列的前n项和Sn,然后就可以求出Tn,再利用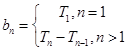 可求{bn}
可求{bn}
的通项公式。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为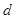 的等差数列;
的等差数列; 是公差为
是公差为 的等差数列(
的等差数列( ).
). = 30,求
= 30,求 是公差为
是公差为 关于
关于 N
N );
);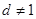 ,试用
,试用
 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数. ,求
,求 的值;
的值; ,求证
,求证 .(本题满分14分)
.(本题满分14分) 中,
中, 是其前
是其前 项和,
项和, ,求:
,求: 及
及 .
. 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且 .
. ,求证:
,求证: ;
; 的前
的前 .
. 是等差数列,
是等差数列,
 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn. 的公比
的公比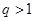 ,
, 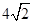 是
是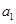 和
和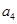 的一个等比中项,
的一个等比中项,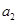 和
和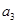 的等差中项为
的等差中项为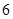 ,若数列
,若数列 满足
满足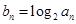 (
(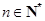 ).
).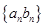 的前
的前 项和
项和 .
. 的前n项和为
的前n项和为 ,且
,且
 ,试求数列
,试求数列 的前
的前 项和.
项和.