题目内容
(本小题满分12分)盒子里装有6件包装完全相同的产品,已知其中有2件次品,其余4件是合格品。为了找到2件次品,只好将盒子里的这些产品包装随机打开检查,直到两件次品被全部检查或推断出来为止。记 表示将两件次品被全部检查或推断出来所需检查次数。
表示将两件次品被全部检查或推断出来所需检查次数。
(I)求两件次品被全部检查或推断出来所需检查次数恰为4次的概率;
(II)求 的分布列和数学期望。
的分布列和数学期望。
(I)所求概率为 (II)分布列如表:
(II)分布列如表: 
2 3 4 5 P 
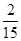


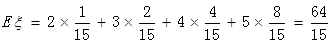
解析试题分析:解:(1)检查次数为4次包含两类情况:
①前3次检查中有一个次品,第4次检查出次品,其概率为 ----2分
----2分
②前4次检查全部是合格品,余下两件必是次品,其概率为 ,----2分
,----2分
所以所求概率为 ,-------5分
,-------5分
(2) 的可能取值为2,3,4,5-----------6分
的可能取值为2,3,4,5-----------6分

 (一个1分)---------10分
(一个1分)---------10分
分布列如表:
所以
2 3 4 5 P 
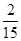


 --------12分
--------12分
考点:古典概型的概率; 的分布列和数学期望。
的分布列和数学期望。
点评:本题需要跟随机变量服从二项分布相区分。要看随机变量是否服从二项分布,关键看是否是重复独立试验。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投 次:在
次:在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在 处的命中率
处的命中率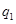 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 | 0 | 2 | 3 | 4 | 5 |
 |  |  |  | 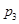 |  |
 的值;
的值; (2) 求随机变量
(2) 求随机变量 的数学期望
的数学期望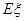 ;
;(3) 试比较该同学选择都在
 处投篮得分超过
处投篮得分超过 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过 分的概率的大小.
分的概率的大小.  ,求:
,求: 上的概率;
上的概率;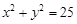 外的概率。
外的概率。 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 。
。  ,求
,求 的一元二次方程
的一元二次方程 .
. ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率; 中,平面区域
中,平面区域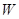 中的点的坐标
中的点的坐标 满足
满足 ,从区域
,从区域 .
. ,
, ,求点
,求点 位于第四象限的概率;
位于第四象限的概率; 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为 ,求
,求 的概率.
的概率.