题目内容
已知数列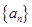 中,
中,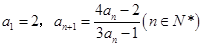 ,设
,设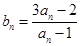 .
.
(Ⅰ)试写出数列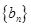 的前三项;
的前三项;
(Ⅱ)求证:数列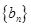 是等比数列,并求数列
是等比数列,并求数列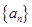 的通项公式
的通项公式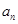 ;
;
(Ⅲ)设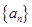 的前
的前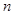 项和为
项和为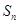 ,
,
求证: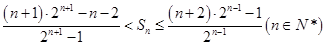 .
.
(Ⅰ)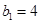 ,
,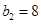 ,
,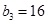 ;(Ⅱ)证明见试题解析,
;(Ⅱ)证明见试题解析,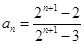 ;(Ⅲ)证明见试题解析.
;(Ⅲ)证明见试题解析.
解析试题分析:(Ⅰ)由递推公式求出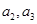 ,再利用
,再利用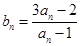 可直接求出
可直接求出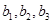 ;(Ⅱ)要证数列
;(Ⅱ)要证数列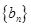 是等比数列,可由数列
是等比数列,可由数列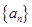 的递推关系
的递推关系 建立起
建立起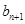 与
与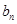 的关系.
的关系.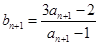
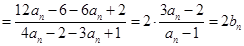 ,从而证得数列
,从而证得数列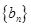 是等比数列. 然后选求出
是等比数列. 然后选求出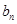 ,由
,由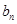 可求出
可求出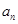 ;(Ⅲ)本题最好是能求出
;(Ⅲ)本题最好是能求出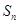 ,但由数列
,但由数列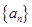 的通项公式可知
的通项公式可知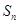 不可求,结合结论是不等式形式可以用放缩法使得和
不可求,结合结论是不等式形式可以用放缩法使得和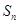 可求,如
可求,如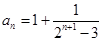
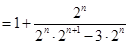
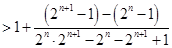
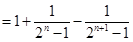
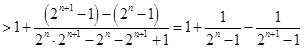 ,又
,又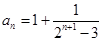
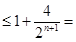
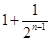 ,即有
,即有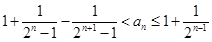 (等号只在
(等号只在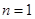 时取得),然后求和,即可证得结论.
时取得),然后求和,即可证得结论.
试题解析:(Ⅰ)由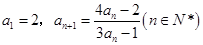 ,得
,得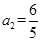 ,
,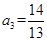 .
.
由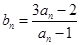 ,可得
,可得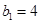 ,
,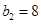 ,
,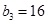 . 3分
. 3分
(Ⅱ)证明:因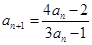 ,故
,故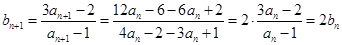 . 5分
. 5分
显然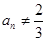 ,因此数列
,因此数列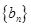 是以
是以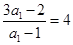 为首项,以2为公比的等比数列,即
为首项,以2为公比的等比数列,即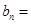
 . 7分
. 7分
解得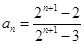 . 8分
. 8分
(Ⅲ)因为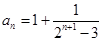
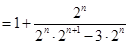
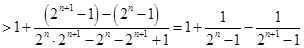 ,
,
所以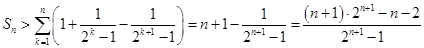 11分
11分
又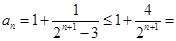
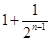 (当且仅当
(当且仅当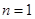 时取等号),
时取等号),
故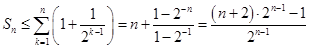 14分[来源
14分[来源
考点:(Ⅰ)数列的项;(Ⅱ)等比数列的定义;(Ⅲ)放缩法.

练习册系列答案
相关题目
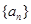 的首项
的首项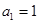 ,公差
,公差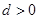 ,且第
,且第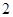 项、第
项、第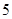 项、第
项、第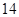 项分别是等比数列
项分别是等比数列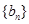 的第
的第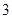 项、第
项、第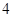 项.
项.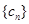 对
对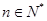 ,均有
,均有 成立,求
成立,求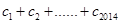 .
.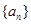 的首项
的首项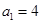 ,公差
,公差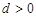 ,且
,且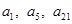 分别是正数等比数列
分别是正数等比数列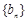 的
的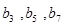 项.
项.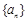 与
与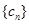 对任意
对任意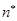 均有
均有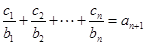 成立,设
成立,设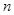 项和为
项和为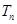 ,求
,求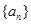 ,公差
,公差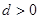 ,前n项和为
,前n项和为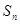 ,
,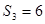 ,且满足
,且满足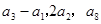 成等比数列.
成等比数列.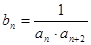 ,求数列
,求数列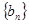 的前
的前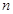 项和
项和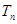 的值.
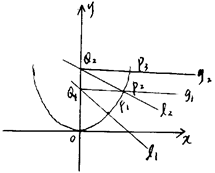
的值.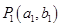 是曲线C:
是曲线C: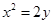 上的一点(其中
上的一点(其中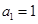 ),过点
),过点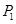 作与曲线C在
作与曲线C在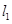 交
交 轴于点
轴于点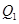 ,过
,过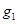 与曲线C在第一象限交于点
与曲线C在第一象限交于点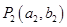 ;再过点
;再过点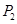 处的切线垂直的直线
处的切线垂直的直线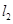 交轴于点
交轴于点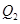 ,过
,过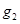 与曲线C在第一象限交于点
与曲线C在第一象限交于点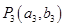 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点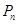 、。(其中
、。(其中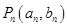 )
)
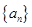 的通项公式。
的通项公式。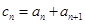 ,且
,且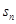 是数列
是数列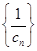 的前
的前 项和,
项和,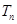 是数列
是数列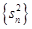 的前
的前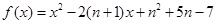 .
.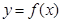 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列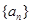 ,求证:
,求证: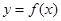 的图像的顶点到
的图像的顶点到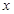 轴的距离构成数列
轴的距离构成数列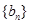 ,求
,求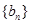 的前
的前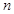 项和
项和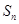 .
.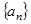 的各项均是正数,其前
的各项均是正数,其前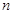 项和为
项和为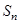 ,满足
,满足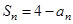 .
.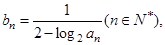 数列
数列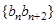 的前
的前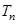 ,求证:
,求证: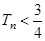 .
.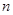 年该生产线设备低劣化值为
年该生产线设备低劣化值为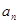 ,求
,求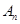 ,当
,当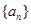 满足
满足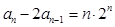
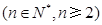 ,且
,且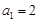 .
.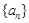 的通项公式;
的通项公式; 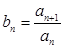 ,当数列
,当数列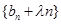 为递增数列时,求正实数
为递增数列时,求正实数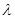 的取值范围.
的取值范围.