题目内容
已知等比数列 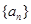 的所有项均为正数,首项
的所有项均为正数,首项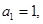 且
且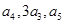 成等差数列.
成等差数列.
(1)求数列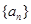 的通项公式;
的通项公式;
(2)数列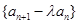 的前
的前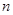 项和为
项和为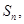 若
若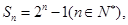 求实数
求实数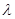 的值.
的值.
(1)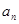 =
=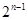
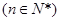 ;(2)
;(2)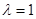 .
.
解析试题分析:(1)利用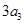 为等差中项列式求解;(2)记
为等差中项列式求解;(2)记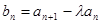 ,证明其为等比数列,求出前
,证明其为等比数列,求出前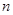 项和,用已知的
项和,用已知的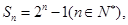 待定系数可得
待定系数可得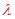 .
.
试题解析:(1)设数列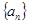 的公比为
的公比为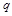 ,由条件得
,由条件得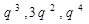 成等差数列,
成等差数列,
所以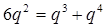 2分
2分
解得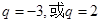
由数列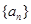 的所有项均为正数,则
的所有项均为正数,则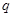 =2 4分
=2 4分
数列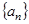 的通项公式为
的通项公式为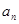 =
=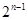
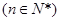 6分
6分
(2)记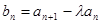 ,则
,则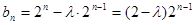 7分
7分
若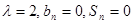 不符合条件; 8分
不符合条件; 8分
若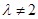 , 则
, 则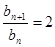 ,数列
,数列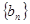 为等比数列,首项为
为等比数列,首项为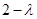 ,公比为2,
,公比为2,
此时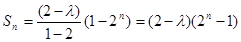 11分
11分
又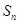 =
=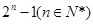 ,所以
,所以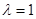 13分
13分
考点:1.等比数列;2.等差数列;3.数列求和.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
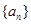 的首项
的首项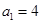 ,公差
,公差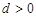 ,且
,且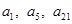 分别是正数等比数列
分别是正数等比数列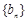 的
的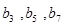 项.
项.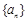 与
与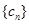 对任意
对任意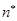 均有
均有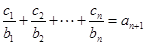 成立,设
成立,设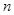 项和为
项和为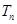 ,求
,求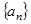 的各项均是正数,其前
的各项均是正数,其前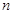 项和为
项和为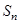 ,满足
,满足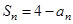 .
.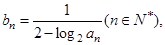 数列
数列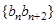 的前
的前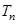 ,求证:
,求证: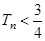 .
.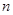 年该生产线设备低劣化值为
年该生产线设备低劣化值为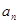 ,求
,求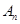 ,当
,当 的前n项和
的前n项和 ,已知对任意的
,已知对任意的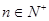 ,点
,点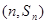 均在函数
均在函数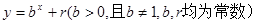 的图像上.
的图像上.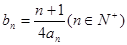 ,求数列
,求数列 的前n项和
的前n项和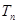 .
.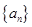 满足:
满足: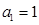 ,
,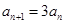 ,
,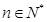 .
. 项和
项和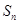 ;
;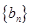 是等差数列,
是等差数列,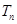 为前
为前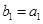 ,
,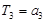 .求
.求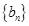 的通项公式,并证明:
的通项公式,并证明: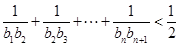 .
.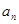 }中,
}中,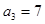 ,又
,又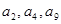 成等比数列.
成等比数列. ,求数列{
,求数列{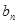 }的前n项和
}的前n项和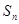 .
.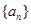 满足
满足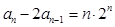
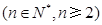 ,且
,且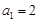 .
.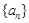 的通项公式;
的通项公式; 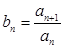 ,当数列
,当数列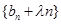 为递增数列时,求正实数
为递增数列时,求正实数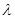 的取值范围.
的取值范围.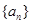 的首项
的首项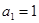 ,公差
,公差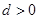 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列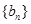 的第2项、第3项、第4项.
的第2项、第3项、第4项.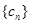 对任意的
对任意的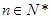 ,均有
,均有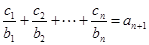 成立,求
成立,求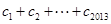 .
.