题目内容
【题目】已知数列![]() 满足
满足![]()
(1)当![]() 时,写出
时,写出![]() 所有可能的值;
所有可能的值;
(2)当![]() 时,若
时,若![]() 且
且![]() 对任意
对任意![]() 恒成立,求数列
恒成立,求数列![]() 的通项公式;
的通项公式;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 分别构成等差数列,求
分别构成等差数列,求![]() .
.
【答案】(1)![]() 或
或![]() 或
或![]() 或
或![]() ;(2)
;(2)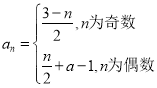 ;(3)
;(3)![]()
【解析】
(1)构造新数列![]() 后分类讨论即可得解;
后分类讨论即可得解;
(2)转化条件得![]() ,
,![]() ,作差得
,作差得![]() ,求出
,求出![]() 后再求出
后再求出![]() 即可得解;
即可得解;
(3)转化条件得![]() ,
,![]() ,分组求和即可得解.
,分组求和即可得解.
(1)当![]() 时,
时,![]() ,
,
即![]() 是以
是以![]() 为首项、
为首项、![]() 为公差的等差数列,
为公差的等差数列,
![]()
![]() ,
,
可得:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() 或
或![]() 或
或![]() 或
或![]() .
.
(2)当![]() 时,
时,![]()
即![]() 是首项为
是首项为![]() .公差为
.公差为![]() 的等差数列,
的等差数列,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() 且
且![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
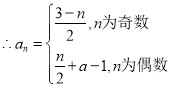 .
.
(3)由己知得![]() ①
①
若![]() ,
,![]() 分别构成等差数列,
分别构成等差数列,
则![]() ,②
,②
![]() ,③
,③
![]() ,④
,④
由②+③得:![]()
![]()
![]() 是等差数列,
是等差数列, ![]() 必为定值,
必为定值,
![]()
![]()
或![]() ,
,
即![]() 或
或![]() ,
,
而由①知![]() ,即
,即![]()
![]() ,
,
即![]() 或
或![]() (舍)
(舍)
![]()
![]() ,
,![]()
![]() .
.
同理,由③+④得:![]()
![]()
![]() 或
或![]() ,
,
由上面的分析可知:![]()
而![]() ,
,![]()
![]() ,
,
即![]() 或
或![]() (舍)
(舍)
![]()
![]()
![]()
![]() ,从而
,从而![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目