题目内容
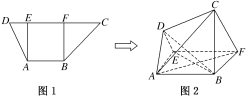
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A,B分别作AE⊥CD,BF⊥CD,垂足分别为E,F.已知DE=1,将梯形ABCD沿AE,BF同侧折起,得空间几何体ADEBCF,如图2.若DE∥CF,CD=![]() ,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为
,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为![]() ?并说明理由.
?并说明理由.
【答案】存在;详见解析
【解析】
由已知可得AE⊥平面DEFC,在梯形![]() 中,根据长度关系可得
中,根据长度关系可得![]() ,建立空间直角坐标系,求出
,建立空间直角坐标系,求出![]() 坐标,进而求出平面ACD的法向量坐标,设
坐标,进而求出平面ACD的法向量坐标,设![]() ,将
,将![]() 坐标用
坐标用![]() 表示,根据线面角公式结合已知,即可求解.
表示,根据线面角公式结合已知,即可求解.
当P为AB的中点时满足条件.理由如下:
∵AE⊥DE,AE⊥EF,DE∩EF=E,∴AE⊥平面DEFC.
取![]() 中点
中点![]() ,连
,连![]() ,
,
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]()
如图,过E作EG⊥EF交DC于点G,
可知GE,EA,EF两两垂直,以E为坐标原点,
以![]() 分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
分别为x轴,y轴,z轴的正方向建立空间直角坐标系,
则A(2,0,0),B(2,2,0),C(0,1,![]() ),
),
D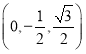 ,
,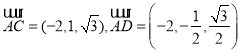 ,
,
设平面ACD的法向量为![]() =(x,y,z),
=(x,y,z),
则![]() ,即
,即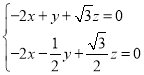 ,
,
令x=1,得![]() .
.
设![]() ,
,
则![]() ,λ∈(0,+∞),
,λ∈(0,+∞),
可得![]() .
.
设CP与平面ACD所成的角为θ,
则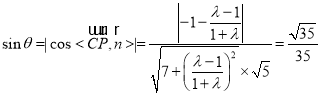 ,
,
整理得![]() ,解得λ=1或λ=
,解得λ=1或λ=![]() (舍去),
(舍去),
∴P为AB的中点时,满足条件.
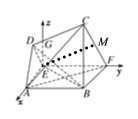

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目