题目内容
在空间直角坐标系O-xyz中,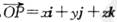 (其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
(其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
①若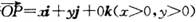 且
且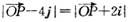 ,则
,则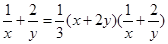
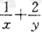 的最小值为
的最小值为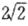 ;
;
②设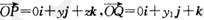 ,若向量
,若向量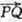 与k共线且
与k共线且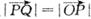 ,则动点P的轨迹是抛物线;
,则动点P的轨迹是抛物线;
③若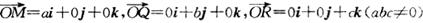 ,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式
,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式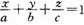 ;
;
④设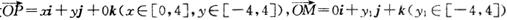 ,
,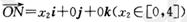 ,若向量
,若向量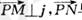 与j共线且
与j共线且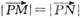 ,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
【答案】
234
【解析】本题考查空间几何与平面向量的交汇。在①中正实数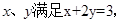 于是
于是
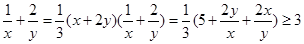 ,在2中向量
,在2中向量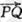 与k共线且
与k共线且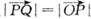 知道
知道 ,并且点P到Q的距离(也就是Q所在直线距离)与P到点O距离相等,定义知P即是在yoz平面表示以定点O为焦点,定直线Q所在直线为准线的抛物线,故正确;在3中平面MQR在坐标面xoy、yoz、zox平面上的直线分别是
,并且点P到Q的距离(也就是Q所在直线距离)与P到点O距离相等,定义知P即是在yoz平面表示以定点O为焦点,定直线Q所在直线为准线的抛物线,故正确;在3中平面MQR在坐标面xoy、yoz、zox平面上的直线分别是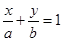 、
、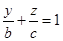 、
、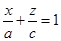 ,故正确;在4中向量
,故正确;在4中向量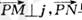 与j共线及点P在XOY坐标平面,得出点N在X轴上,点M在YOZ坐标平面的直线Z=1上且与点P的y坐标等,再
与j共线及点P在XOY坐标平面,得出点N在X轴上,点M在YOZ坐标平面的直线Z=1上且与点P的y坐标等,再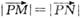 坐标化可以知道
坐标化可以知道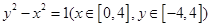 ,故正确
,故正确

练习册系列答案
相关题目