题目内容
6.当n≥3,n∈N时,对于集合M={1,2,3,…,n},集合M的所有含3个元素的子集分别表示为N1,N2,N3,…NM(n)-1,NM(n),其中M(n)表示集合M的含3个元素的子集的个数.设pi为集合Ni中的最大元素,qi为集合Ni中的最小元素,1≤i≤M(n),记P=p1+p2+…+pM(n)-1+pM(n),Q=q1+q2+…qM(n)-1+qM(n).(1)当n=4时,分别求M(4),P,Q;
(2)求证:P=3Q.
分析 (1)根据题意,分析可得当n=4时,M(4)=4,即可以写出其4个子集,结合题意可得P与Q的值;
(2)根据题意,分析易得3≤pi≤n,pi∈Z,且以3为最大元素的子集有${c}_{2}^{2}$个,类推可得以4、5、…、k为最大元素的子集的数目,计算可得P的值;进而分析可得1≤qi≤n-2,qi∈Z,以1、2、…k…(n-2)为最小元素的子集数目,即可得Q的值,两者相加可得P+Q=4${C}_{n+1}^{4}$=4Q,即得证明.
解答 解:(1)当n=4时,M(4)=${c}_{4}^{3}$=4,
4个子集分别为{1,2,3};{1,2,4};{1,3,4};{2,3,4},
则P=3+4+4+4=15,Q=1+1+1+2=5;
(2)证明:显然3≤pi≤n,pi∈Z,且以3为最大元素的子集有${c}_{2}^{2}$个,
以4为最大元素的子集有${C}_{3}^{2}$个,以5为最大元素的子集有${C}_{4}^{2}$个,…以k(3≤k≤n)为最大元素的子集有${c}_{k-1}^{2}$个,
P=P1+P2+…+PM(n-1)+PM(n)=3×${C}_{2}^{2}$+4×${C}_{3}^{2}$+…+n${C}_{n-1}^{2}$①,
∵k${C}_{k-1}^{2}$=k$\frac{(k-1)(k-2)}{2}$=3${C}_{k}^{3}$(k=3,4,…n),
∴P=3(${C}_{3}^{3}$+${C}_{4}^{3}$+…+${C}_{n}^{3}$)=3(${C}_{4}^{4}$+${C}_{4}^{3}$+…+${C}_{n}^{3}$)+3(${C}_{5}^{4}$+${C}_{5}^{3}$+…+${C}_{n}^{3}$)=3(${C}_{6}^{4}$+${C}_{6}^{3}$+…+${C}_{n}^{3}$)=3${C}_{n+1}^{4}$,
显然1≤qi≤n-2,qi∈Z,以1为最小元素的子集有${C}_{n-1}^{2}$个,以2为最小元素的子集有${C}_{n-2}^{2}$个,以3为最小元素的子集有${C}_{n-3}^{2}$个,…
以k为最小元素的子集有${C}_{n-k}^{2}$个,…
以(n-2)为最小元素的子集有${C}_{2}^{2}$个,
Q=q1+q2+…qM(n)-1+qM(n)=(n-2)${C}_{2}^{2}$+(n-3)${C}_{3}^{2}$+…k${C}_{k}^{2}$+…${C}_{n-1}^{2}$,
①+②可得:P+Q=(n+1)(${C}_{2}^{2}$+${C}_{3}^{2}$+${C}_{4}^{2}$+…+${C}_{n-1}^{2}$)
=(n+1)(${C}_{3}^{3}$+${C}_{3}^{2}$+${C}_{4}^{2}$+…+${C}_{n-1}^{2}$)=4${C}_{n+1}^{4}$,
所以P=3Q.
点评 本题考查组合数的性质、运算,涉及子集的性质,解题的关键是分析满足条件的子集的数目以及运用组合数公式进行计算.

①若α⊥γ、β⊥γ则α∥β;
②若m?α、n?α、m∥β、n∥β则α∥β;
③若α∥β、γ∥β则γ∥α;
④若α⊥β、m⊥β则m∥α;
⑤m⊥α、n⊥α则m∥n中,
真命题个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | a>b>c | B. | a<b<c | C. | c>a>b | D. | b>a>c |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
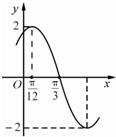 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.