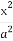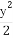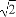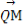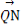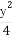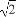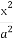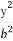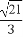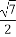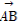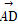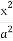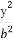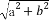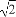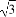题目内容
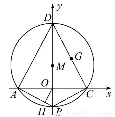
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为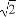 ,且过点P(4,-
,且过点P(4,-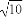 ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: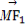 ·
·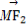 =0.
=0.
(3)求△F1MF2的面积.
(1) x2-y2=6 (2)见解析 (3)6
【解析】(1)∵e=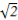 ,
,
∴可设双曲线方程为x2-y2=λ(λ≠0).
∵过点P(4,-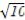 ),∴16-10=λ,即λ=6.
),∴16-10=λ,即λ=6.
∴双曲线方程为x2-y2=6.
(2)方法一:由(1)可知,双曲线中a=b=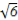 ,
,
∴c=2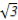 ,∴F1(-2
,∴F1(-2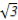 ,0),F2(2
,0),F2(2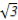 ,0).
,0).
∴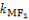 =
= ,
,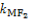 =
=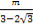 ,
,
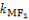 ·
·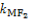 =
=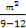 =-
=-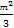 .
.
∵点M(3,m)在双曲线上,
∴9-m2=6,m2=3.
故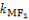 ·
·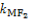 =-1,∴MF1⊥MF2.
=-1,∴MF1⊥MF2.
∴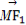 ·
·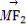 =0.
=0.
方法二:∵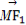 =(-3-2
=(-3-2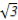 ,-m),
,-m),
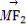 =(2
=(2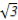 -3,-m),
-3,-m),
∴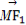 ·
·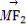 =(3+2
=(3+2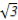 )×(3-2
)×(3-2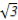 )+m2=-3+m2.
)+m2=-3+m2.
∵M(3,m)在双曲线上,
∴9-m2=6,即m2-3=0.
∴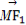 ·
·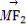 =0.
=0.
(3)△F1MF2的底|F1F2|=4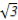 ,
,
△F1MF2的边F1F2上的高h=|m|=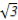 ,
,
∴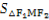 =6.
=6.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目