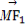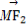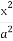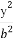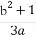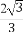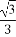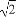题目内容
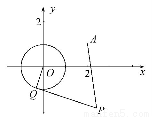
如图,
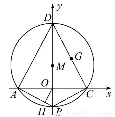
在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0.
(2)若四边形ABCD的面积为8,对角线AC的长为2,且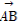
·
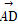=0,求D2+E2-4F的值.
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判断点O,G,H是否共线,并说明理由.
(1)见解析 (2)64 (3) O,G,H三点必定共线，理由见解析
【解析】(1)方法一:由题意,原点O必定在圆M内,即点(0,0)代入方程x2+y2+Dx+Ey+F=0的左边所得的值小于0,于是有F<0,即证.
方法二:由题意,不难发现A,C两点分别在x轴正、负半轴上.设两点坐标分别为A(a,0),C(c,0),则有ac<0.对于圆的方程x2+y2+Dx+Ey+F=0,当y=0时,可得x2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,于是有xAxC=ac=F.
因为ac<0,故F<0.
(2)不难发现,对角线互相垂直的四边形ABCD的面积S=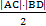
,因为S=8,|AC|=2,可得|BD|=8.
又因为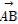
·
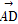=0,所以∠BAD为直角,又因为四边形是圆M的内接四边形,故|BD|=2r=8⇒r=4.
对于方程x2+y2+Dx+Ey+F=0所表示的圆,
可知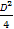
+
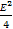-F=r2,所以D2+E2-4F=4r2=64.
(3)设四边形四个顶点的坐标分别为A(a,0),B(0,b),C(c,0),D(0,d).
则可得点G的坐标为(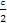
,
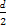),即
=(,).
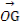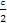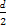又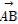=(-a,b),且AB⊥OH,故要使G,O,H三点共线,只需证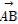·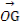=0即可.
而·=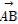
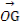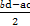,且对于圆M的一般方程x2+y2+Dx+Ey+F=0,
当y=0时可得x2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,
于是有xAxC=ac=F.
同理,当x=0时,可得y2+Ey+F=0,其中方程的两根分别为点B和点D的纵坐标,于是有yByD=bd=F.
所以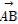·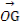==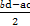0,即AB⊥OG.
故O,G,H三点必定共线.
