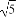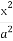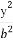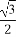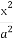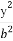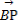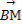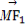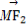题目内容
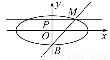
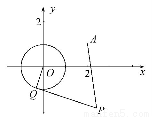
如图,椭圆C: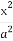 +
+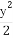 =1的焦点在x轴上,左右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=
=1的焦点在x轴上,左右顶点分别为A1,A,上顶点为B,抛物线C1,C2分别以A,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线y=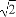 x上一点P.
x上一点P.
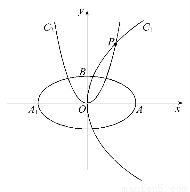
(1)求椭圆C及抛物线C1,C2的方程.
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M,N,已知点Q(-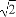 ,0),求
,0),求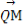 ·
·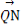 的最小值.
的最小值.
(1) 椭圆C: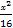 +
+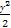 =1 C1:y2=16x C2:x2=4
=1 C1:y2=16x C2:x2=4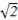 y (2)
y (2) 
【解析】(1)由题意A(a,0),B(0,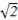 ),设抛物线C1的方程为y2=4ax,抛物线C2的方程为x2=4
),设抛物线C1的方程为y2=4ax,抛物线C2的方程为x2=4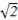 y,由
y,由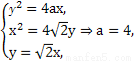 P(8,8
P(8,8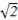 ),∴椭圆C:
),∴椭圆C: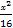 +
+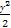 =1.
=1.
抛物线C1:y2=16x,
抛物线C2:x2=4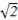 y.
y.
(2)由(1)得直线OP的斜率为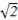 ,
,
∴直线l的斜率k=- ,
,
设直线l:y=- x+b,
x+b,
由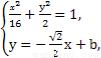 消去y,得
消去y,得
5x2-8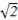 bx+8b2-16=0.
bx+8b2-16=0.
∵动直线l与椭圆C交于不同的两点,
∴Δ=128b2-20(8b2-16)>0.
∴-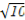 <b<
<b<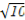 .
.
设M(x1,y1),N(x2,y2),
∴x1+x2= ,x1x2=
,x1x2=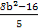 .
.
y1y2=(- x1+b)(-
x1+b)(- x2+b)
x2+b)
=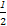 x1x2-
x1x2-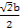 (x1+x2)+b2=
(x1+x2)+b2=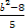 .
.
∵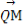 =(x1+
=(x1+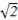 ,y1),
,y1),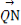 =(x2+
=(x2+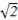 ,y2),
,y2),
∴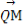 ·
·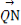 =(x1+
=(x1+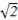 )(x2+
)(x2+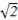 )+y1y2
)+y1y2
=x1x2+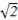 (x1+x2)+2+y1y2
(x1+x2)+2+y1y2
=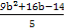 ,
,
∵-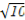 <b<
<b<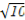 ,
,
∴当b=-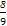 时,
时,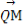 ·
·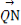 取得最小值,其最小值为
取得最小值,其最小值为
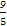 ×(-
×(-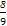 )2+
)2+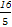 ×(-
×(-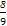 )-
)-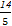 =-
=-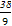 .
.

练习册系列答案
相关题目