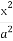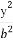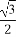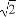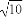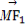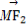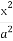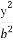Question

给定椭圆C: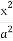+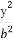=1(a>b>0),称圆心在原点O,半径为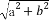的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(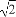,0),其短轴上的一个端点到F的距离为.

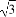(1)求椭圆C的方程和其“准圆”的方程.

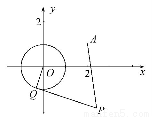
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.

①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;

②求证:|MN|为定值.

 

Answer 1

(1) +y2=1 x2+y2=4

(2) ①y=x+2,y=-x+2 ②见解析

【解析】(1)∵c=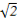,a=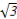,∴b=1.

∴椭圆方程为+y2=1,

准圆方程为x2+y2=4.

(2)①因为准圆x2+y2=4与y轴正半轴的交点为P(0,2),

设过点P(0,2)且与椭圆有一个公共点的直线为y=kx+2,所以由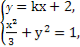消去y,

得(1+3k2)x2+12kx+9=0.

因为椭圆与y=kx+2只有一个公共点,

所以Δ=144k2-4×9(1+3k2)=0,解得k=±1.

所以l1,l2的方程分别为y=x+2,y=-x+2.

②(ⅰ)当l1,l2中有一条无斜率时,不妨设l1无斜率,

因为l1与椭圆只有一个公共点,

则其方程为x=±.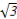

当l1方程为x=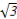时,

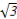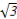此时l1与准圆交于点(,1),(,-1),

此时经过点(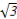,1)(或(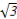,-1))且与椭圆只有一个公共点的直线是y=1(或y=-1),

即l2为y=1(或y=-1),显然直线l1,l2垂直;

同理可证l1方程为x=-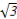时,直线l1,l2垂直.

(ⅱ)当l1,l2都有斜率时,设点P(x0,y0),

其中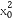+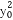=4.

设经过点P(x0,y0)与椭圆只有一个公共点的直线为y=t(x-x0)+y0,

则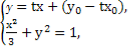消去y,

得(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.

由Δ=0化简整理得:(3-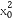)t2+2x0y0t+1-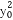=0.

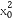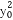因为+=4,

所以有(3-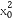)t2+2x0y0t+(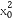-3)=0.

设l1,l2的斜率分别为t1,t2,

因为l1,l2与椭圆只有一个公共点,

所以t1,t2满足上述方程(3-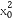)t2+2x0y0t+(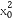-3)=0,

所以t1·t2=-1,即l1,l2垂直.

综合(ⅰ)(ⅱ)知:因为l1,l2经过点P(x0,y0),

又分别交其准圆于点M,N,且l1,l2垂直,

所以线段MN为准圆x2+y2=4的直径,

所以|MN|=4.