题目内容
【题目】已知直线l的参数方程为![]() (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)直线l与曲线C交于AB两点,P(1,3),求![]() 的值.
的值.
【答案】(1)y=2x+1,![]() .(2)
.(2)![]()
【解析】
(1)消去参数![]() ,即可求得直线l的普通方程;利用公式,即可求得曲线C的直角坐标方程;
,即可求得直线l的普通方程;利用公式,即可求得曲线C的直角坐标方程;
(2)求得直线的标准参数方程,联立曲线![]() 的普通方程,得到关于
的普通方程,得到关于![]() 的一元二次方程,利用参数
的一元二次方程,利用参数![]() 的几何意义,即可求得结果.
的几何意义,即可求得结果.
(1)直线l的参数方程为 ![]() (t为参数),
(t为参数),
消去参数,可得直线l的普通方程y=2x+1,
曲线C的极坐标方程为![]() ,即8ρ2sin2θ+ρ2=9,
,即8ρ2sin2θ+ρ2=9,
∴x2+y2+8y2=9,
∴曲线C的直角坐标方程为![]() y2=1.
y2=1.
(2)直线的参数方程改写为 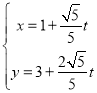 (t为参数),
(t为参数),
代入![]() y2=1,
y2=1,
可得![]() t2
t2![]() t+73=0,
t+73=0,
故t1+t2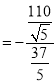 ,t1t2
,t1t2![]() ,
,
![]()
![]() .
.
∴当直线l与曲线C相交时,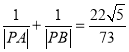 .
.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目